Full Page

On the relation of Fuzzy subsets, Postean and Boolean lattices .

The λ-rainbow lattices. Transfinite Fuzzy subsets.

By Dr Constantine E. Kyritsis

University of Portsmouth

Department of Mathematics and Computer Science

§ Ο. Introduction. In this paper it is attempted to relate the definitions of the fuzzy subset lattices with the other classical definitions of Postean and Boolean lattices in the context of Universal algebra. In particular it is obtained a kind of equivalence (mutual isomorphic representations) of the fuzzy subsets, Postean and Boolean lattices. (corollaries 28,29,30.).This unification is worked out with the axiomatic introduction of the λ-rainbow lattices (§1). In order to obtain these results, it is used the extended Stone's representation theorem (theorem 1). The way that this theorem is formulated makes use of the extended Birkhoff-Stone theorem (corollary 21). It is given new and more enlightening and simpler proofs for both theorems. They are discussed partial abelian semigroups, abelian groups, rings and modules that are also lattices. It is Introduced the concept of compatibility of the order relation and the algebraic structure. The previous equivalence theorems have important consequences in a kind of equivalence, up-to-lattices of the Fuzzy, 3-valued and 2-valued Logic. It is possible obtain the fuzzy logic as a general Logic (according to [J. Mesenquer 1987]). By introducing an ordering it is possible to investigate the relation of a general Logic, the Fuzzy, the 3-valued and the 2-valued Logic.

In the paragraph §2 is introduced the transfinite real, complex, quaternion Fuzzy subset lattices. They can be considered as a kind of Arithmetisation of the abstract λ-Fuzzy lattices. They have special good properties that can be understood only by a familiarity with the transfinite real numbers.

§1 The λ-rainbow (or fibber) lattices and the λ-Fuzzy subsets lattices.

As it is known the category of Boolean lattices has been extensively studied, mainly because of its applications in Logic. The attempts to give alternative formulations of Logic led to other categories of lattices, like the Postean lattices (see e.g.[Carvallo M.1968],[Lukasiewicz,J1920],[Post E.L. 1921]), or the lattices of Fuzzy subsets (see e.g.,[Zadeth,L.A 1965]). A closer study of the Boolean, Postean Fuzzy -subsets, modular- complemented lattices leads naturally to a broad category of lattices which we define axiomatically in this paragraph and we call rainbow or fibber lattices. In conceiving the idea of rainbow lattices I was partly influenced at least by the terminology, of the Kantian ideas of transcendental analytic and synthetic logic and of Aristotle’s term of “colors of the word”. As we shall see transfinite numbers appear also.

Remark: If a lattice has minimum and maximum elements we denote them with 0,1 respectively.

We are now in a position to define the rainbow (or fibber) lattices: Let an non-empty order type which we denote by λ. Let a lattice, which we denote by L such that:

The λ-rainbow (or fibber) axioms:

A₀: The order type λ is a sublattice of L and the L has 0 and 1.

A₁: If αÎλ α¹0 and for a xÎL it holds xÙa=0 then x=0.

A₂: If α Îλ, α¹1 and for a xÎL holds xÚa=1 then x=1.

The spectral axioms:

For every xÎL there is a λ-family of elements of L {x_α| αÎλ} which, is called the λ-spectrum of the x, such that:

B₀: The previous representation is called the λ-spectral expansion of x.

B₁: If α₁¹α₂ for two λ-indices of the spectrum of x, then x_α1Ù x_α2 =0

B₂: For the λ-spectrum of x holds .

Definition 1. A Lattice that satisfies the axioms A₀, A₁, A₂, B₀, B₁, B₂ as above, is called a λ-rainbow (or λ-fibber) llattice.

Remark 2: If the λ is the order type of an ordinal number α, we write simply a-rainbow lattice. If λ=3={-1<0<+1} and the L is furthermore distributive we get the definition of a Postean lattice (see e.g.[Carvallo ,M.1968],[Lukasiewicz,J.1920],[Post, E.L. 1921]). In other words a Postean lattice is defined as a distributive 3-rainbow lattice. We shall prove that the Fuzzy-subsets lattices are λ-rainbow lattices .We shall describe in the first a way to construct λ-rainbow lattices from λ-order types.

Remark. Let us suppose that the order type is at the same time a commutative partial semigroup such that the order and the operations are compatible: In other words if we denote by i the identity mapping and for two elements a, b the sums i (a)+i(b), i(aÚb)+i(aÙb) exist then it holds that i(aÚb)+i(aÙb)=i(a)+i(b). In other word, again the identity mapping is a (partial semigroup valued) lattice valuation .Then a λ-rainbow lattice on such a λ is called rainbow lattice with algebraic fibber. If the partial semigroup λ, is a category, commutative group, ring, field, module, or vector space, then we put this term before the term algebraic.

Lemma 3. The (direct) product in the category of lattices of the order type λ with extremes 0,1, X-times where X is an arbitrary set, is a distributive λ-rainbow lattice.

Proof: The order type λ is contained as a sublattice in the , as the element with all the coordinates equal.

Thus the axioms A₀, A₁, A₂ are satisfied .We define as the λ-spectrum of an element x of the elements {x_α| αÎλ} such that the x_α is the element with all the coordinates equal to 0 except at the places where the coordinates of x are equal to a where it is equal, to 1. It is direct that the axioms B₀, B₁, B₂ are satisfied. The order type λ is a distributive lattice. Obviously the same holds for the (direct) product Q.E.D.

Remark 4. The λ-rainbow lattices with extremes 0,1,

(in other words as in lemma 3 ) are the λ-Fuzzy subsets lattices

Corollary 5. The λ-Fuzzy-subsets lattices are distributive, λ-rainbow lattices.

Proof: A λ-Fuzzy-subset lattice on a set X is exactly the (direct), product in the category of lattices ;Where the λ is, an order type .Thus we apply the previous Lemma Q.E.D.

Lemma 6. Let two order types λ₁, λ₂ such that λ₁ £ λ₂ (the λ is isomorphic to a suborder type of λ₂).The lattice 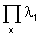is isomorphic to a sublattice of .

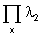Proof :1Direct from the definitions and that λ₁ £ λ₂. Q.E.D.

Lemma 7. A lattice is complemented if and only if it is a 2-rainbow lattice.

Remark 8. A lattice is called complemented if it has extremes, 0,1 and for any element x there is an element x' such that, xvx'=1 and x^x'=0 .The x' is called the complement of x .(See also [v Neumann J.1960] part 1 ch 1 axiom v pp 2 or the paper with the same title in his collected works ) .It is not postulated uniqueness of the complement of an element .

Proof : The order type λ is the two element set {0,1} thus the, order type of 2. Thus the axioms A₀, A₁, A₂ are satisfied .As the {0,1}spectrum of any element x we define the two element set {x₀, x₁ } with x₀=x' and x₁=x .By x' we denote the complement of x . It holds by the definition of the complement that (0^x₀) v(1^ x₁ )=(0^x')v(1^ x)=0vx=x ;and x₀^x₁ =x'^x=0, x₀ vx₁ =x' vx=1.

Thus the axioms B₀, B₁, B₂ are satisfied. Conversely in every 2-rainbow lattice the x₀ can be taken as a complement of x=x₁. Q.E.D.

Corollary 9. A lattice is a Boolean lattice if and only if it is, a distributive 2-rainbow lattice.

Proof: Direct from the previous lemma and that every Boolean, lattice is defined as a complemented (distributive) lattice. Q.E.D.

§2 .The transfinite real, complex, quaternion Fuzzy subsets and lattices.

Remark 10. In the next we introduce the transfinite real, complex,, quaternion Fuzzy subsets .We shall examine at first the elementary cases of the real, complex and quaternion fuzzy subsets. In the definition of the ordinary [0,1]-fuzzy subsets (see e.g.[Zadeth,,L.A.1965]) what matters is the interval [0,1] as an order type and not what numbers are the extremes of it. Let us consider the 2-point compactification of the linearly ordered field of the real numbers , where the -¥, +¥ are the minimum and maximum of . As it is known the is order isomorphic order type to the order type [0,1]. Therefore the [0,1]-Fuzzy subsets can be considered as -Fuzzy subsets. The latter form is some how more convenient as we can make use of the algebraic structure of the field . Furthermore negative values of the index or characteristic function of a fuzzy subset can appear.

It is very natural to substitute the linearly ordered (commutative) field with the field of the complex numbers C or the (non-commutative) field of the quaternion numbers H. (See also [v.Weizacker C.F.-Sheibe,E. Sussmann G. 1958]. Actually we have to use the compactifications of them . Thus the elements of the products in the category of sets , where the x is an arbitrary set, are the real ,complex and quaternion Fuzzy subsets of x .The norm of the characteristic functions of them give real Fuzzy subsets. But the advantage of the complex and quaternion Fuzzy subsets is that besides their real norm they have respectively a phase e^i¶, e^q¶ (where i is the imaginary unit and the q is a unit vector of the Euclidean space R³). The way to define the transfinite real, complex and quaternion Fuzzy subsets is plausible and formalises a non-Archimedean phased Fuzziness.It is to be understood that the next arguments do not have to depend on the [Conway J.H.1976],[Robinson A. 1966].It can be proved that all the three different techniques of the transfinite real numbers, the surreal numbers and the ordinal real numbers give by inductive limit or union the same class of numbers known already as the class No. This class can be called the totally ordered, finitary Newton-Leibniz realm of numbers. Till the moment that this shall be understood we can be content with the transfinite real numbers in [Glayzal A.1937].Although logically not necessary, any additional references to the ordinal real numbers shall be in parenthesis and shall not affect the arguments. The author believes that the Ordinal real numbers shall be indispensable, in the future, for numerical and quantitative applications of mathematics to other sciences.

The transfinite real numbers were defined at first by A.Glayzal in 1937(!) (see [Glayzal A.1937] ). His technique was what it is now known as formal power series fields. His main idea was to define by formal power series fields, Archimedean complete (although non-Archimedean) linearly ordered fields. The concept of non-Archimedean order is known in the process management of operating systems in computer science and in operation research (Goal programming) as pre-emptive prioritisation.

(It it can proved that they are fundamental (Cauchy) complete (in the order topology ) and Dedekind complete. I repeat that the reader can be content with their definition in [Glayzal A.1937] which we repeat concisely .Let any order type which we denote by λ. Let the Lexicographic product of λ-copies of the field of the real numbers R, which we denote by . Its elements are the elements of the Group-product which have zero all the components except on a well-ordered subset of λ. This subset is called as usually the support of the element. The group is a linearly ordered group in the lexicographic ordering .The formal power series field is defined as the transfinite real numbers of Archimedean base λ. Let us denote by R (R (λ) ) the real closure of the transfinite real numbers ; it can be obtained by adjunction of the square roots of its positive elements But the R (λ) is a formal power series field, thus it contains the n-roots of its positive elements (see [v.Neumann] B.H. 1949] 4.91 Corollary pp 211). In other words it is Pythagorean complete. Thus R (R (λ) ) = R (λ).

Consequently its extensions of degree 2 with the imaginary unit C (λ) = R (λ) (i) is also algebraically closed .The algebraically closed and formal power series field C (λ) we call transfinite complex numbers of Archimedean base λ . It holds obviously that . Similarly the field that is obtained by the quaternion extension of R (λ) ,which is the field is called the transfinite quaternion numbers of Archimedean base λ. Let us consider the extensions of them

where the -¥, +¥ are the minimum and maximum of the order type .

Definition 11. The products in the category of sets, where the X is an arbitrary set ,are called the transfinite, real ,complex, quaternion Fuzzy subsets of X.

Remark 12. The norm of the transfinite real ,complex ,quaternion numbers of some Archimedean base λ , is defined as in the minimal case of the real, complex ,and quaternion numbers. Only that the norm is not a positive real number but a transfinite positive real number. By taking the norm , the transfinite real, complex, quaternion Fuzzy subsets define -fuzzy subsets. Such (real) Fuzzy subsets we call transfinite Fuzzy subsets. They are special Fuzzy subsets, since the order types have special good properties; (fundamental completeness in the order topology, Dedekind completeness , they contain initial segments of the ordinal numbers e.t.c.).

The applications of the (real) transfinite Fuzzy subsets are as the applications of the general Fuzzy subsets and even better.

Remark. By the way that the transfinite real numbers are defined (over an arbitrary order type which is its Archimedean base) it is clear that any order type λ is order embeddable in some field of transfinite real numbers .Therefore after lemma 6 every λ-Fuzzy subsets lattice is isomorphic with the a sublattice of some transfinite real Fuzzy subsets lattice.

Corollary (The transfinite Fuzzy subsets lattice reduction )

Any λ-Fuzzy subsets lattice is isomorphic with a sublattice of some transfinite (real) Fuzzy subsets lattice.

Remark. It can be proved that any order type can be constructed by the ordinal numbers. This constitutes a genuine and better Arithmetisation of the λ-Fuzzy subsets).

§3 Rings that are also lattices. Auxiliary rings.

As it is known J.v.Neumann has studied the orthomodular 2-rainbow lattices that appear as lattices of projections in Hilbert spaces. He has also introduced and studied a special category of modular 2-rainbow lattices that he called continuous geometry (see [v.Neumann,J. 1960]). He proved that such lattices admit valuations in the real numbers .He proved that the modular 2-rainbow lattices have an up-to-isomorphism representation as lattices of ideals of rings. The ring that corresponds to every such lattice is called auxiliary ring (see [v.Neumann J.1960] part ii). This technique is not little laborious.

In the case of the Boolean lattices the auxiliary ring is again the Boolean algebra and the ring operations are x+y=(x^y')v(x'^y) and x.y=x^y .Any element of the Boolean lattice corresponds to the principal ideal that it defines . The principal lattice-ideals and the principal ring-ideals coincide. The correspondence is a lattice isomorphism. The present representation theorem gives also a result of the same type. In other words an auxiliary ring appears also. Thus it can be also considered as a J.v.Neumann- type representation.

Definition 13. Let us denote a lattice by L and a ring by R. The ring R is called auxiliary to the lattice L if there is an isomorphism of L with a lattice of ideals of R.

Such an isomorphism is called a J.v.Neumann-type representation.

Remark 14: By the Stone's representation theorem we deduce that every Boolean lattice is isomorphic with a sublattice of the Power- set P(X) which is also a lattice of a set X .Considering the characteristic functions of the subsets of X we deduce that every Boolean lattice is isomorphic with a sublattice of the abelian Ζ₂-linear algebra . The product is considered in the category of rings and simultaneously in the category of lattices .The Galois field Ζ₂ is considered as a lattice with the ordering 0<1.

It might be interesting to have a closer look to modules and rings that are also lattices (see also remark after remark 2).

Let a ring R and an lattice ordering on it .We do not suppose any compatibility of the ordering and the ring operations.

E.g. we may consider the rings Z_n with the linear ordering

0<1/_π-1<1/_π-2<…<1/₂<1.

Or we may consider any linearly ordered ring e.g. the field real numbers.

The (direct) product over a set of indices X simultaneously

in the category of rings , and of lattices is a ring which is also a lattice .In the previous examples the are Z_n-modules and rings which are also distributive n-rainbow lattices.

If n=p where p is a prime natural number then the distributive p-rainbow lattice is also a Z_p-linear algebra.

In these commutative Z_p-linear algebras holds that x^P=x and px=0 (it is of, characteristic n) ;which is a consequence of the Fermat theorem for the Galois fields Z_p.

The identity function has the property that xvy + xÙy = x+y.

Thus it is a Lattice valuation with values in the commutative semigroup . For n=2 or 3 the relation of the lattice-operations and the ring operations are:

éa.b if a≠b éa+b -a.b if a≠b

a^b = ëa if a=b avb= ëa if a=b .

The lattices p=2,3 have as auxiliary rings again the .

To every element corresponds the principal ring-ideal that it defines. The principal lattice-ideals and the principal ring-ideals ,coincide.

§4 The inverse of the Birkhoff-Stone theorem in lattices

Definition 15. A set , that we denote by Θ , of congruencies in a lattice,

that we denote by L, is said that it is separating iff for any two elements x,yÎL with x ≠y there is a congruence ¶ÎΘ such that x≠y mod¶.

Remark 16: If the lattice L has minimum, that we denote by 0, then as it is known to every congruence ¶ corresponds an ideal that we denote by Ι_¶, which is the equivalence class of 0. Thus we have also the next definition :

Definition 17 Let a lattice, be denoted by L, and a set of ideals of it, be denoted by I. It is said that the I is a separating set of ideals iff for any two x, yÎL with x≠y there is an ideal iÎI such that xÎi and yÏi.

Definition 18.Let a lattice, be denoted by L. The set of its prime ideals we denote by SpecL and we call the spectrum of the lattice L.

Definition 19. A lattice, which is denoted by L, is said that it is with separating spectrum iff the set of ideals SpecL is separating in the L.

Theorem 20. (The extended Birkhoff-Stone theorem)

A lattice is with separating spectrum if and only if it is distributive .

Proof: see [Sirkoski,R 1969] Appendix 6 §13 first page of the paragraph

Q.E.D.

The Stone's representation theorem makes use of the fact that the spectrum of a Boolean lattice coincides with the set of its maximal ideals and that and the Birkhoff-Stone theorem which gives that any distributive lattice is with separating spectrum .

The Stone's representation theorem can be extended to any

lattice with separating spectrum .

Theorem 21. (The extended Stone's isomorphic representation theorem ).

Let us denote by L a lattice with separating spectrum.

There is an isomorphism of L with a lattice of sets.

Proof: See [Birkhof,G 1967] ,or [Gratzer,G 1979] ,or[Sikorski,R 1969] or any comprehensive book about

lattices. Q.E.D.

Corollary 22. (J.v.Neumann-type isomorphic representation )

Every distributive lattice has an auxiliary (abelian) ring.

Proof: The distributive 2-rainbow lattices by the last remark of §3 have auxiliary ring the same set as a product abelian ring.

Q.E.D.

The next corollaries are results about the relation of the Boolean, Postean, and Fuzzy-subset lattices.

Corollary 23. (The Z₂ reduction)

Every Postean and Fuzzy-subset lattice is isomorphic to a lattice of sets and has an auxiliary ring.

Corollary 24. Every distributive λ-rainbow lattice is isomorphic with a sublattice of a λ’-rainbow lattice , for every order type λ’ with extremes, in other words with a sublattice of a λ’-Fuzzy subsets lattice.

Proof: We apply the theorem 20 and the lemma 6 .The Z₂ 2-rainbow lattice is the minimal (or trivial ) rainbow lattice.

Corollary 25. (The λ-Fuzzy representation of distributive λ-rainbow lattices)

Every distributive λ-rainbow lattice is isomorphic with a sublattice of a λ-Fuzzy lattice.

Corollary Every distributive λ-rainbow lattice is isomorphic with a sublattice of a transfinite (real) Fuzzy subset lattice.

Proof: We apply the transfinite Fuzzy reduction of the Fuzzy subsets lattices of §2 and the previous lemma.

Corollary 26. (The Z₃ reduction). Every distributive lattice and in particular every Fuzzy-subset lattice is isomorphic with a sublattice of a Postean lattice of type .

Corollary 27. (The Fuzzy-reduction)

Every distributive lattice isomorphic with a sublattice of a Fuzzy-subset lattice

Corollary 28. (The Z₂↔Fuzzy equivalence)

Every Boolean lattice is isomorphic with a sublattice of a Fuzzy-subset lattice and every Fuzzy-subset lattice is isomorphic with a sublattice of a Boolean lattice.

Corollary 29. (The Z₂↔Z₃ equivalence)

Every Boolean lattice is isomorphic with a sublattice of a Postean lattice and every Postean lattice is isomorphic with a sublattice of a Boolean lattice.

Corollary 30. (The Z₃↔Fuzzy equivalence)

Every Postean lattice is isomorphic with a sublattice of a Fuzzy-subset lattice and every Fuzzy-subset lattice is isomorphic to a sublattice of a Postean lattice.

Corollary 31. (The equivalence up-to-lattices of the Fuzzy, 3-valued and 2-valued Logic.)

The Fuzzy, 3-valued, 2-valued Logics are up-to-lattices equivalent in the sense that there are mutual isomorphic representations of the logical (lattice) orders of them.

(See also [A.I.Appudia etc 1977],[J.Barwise,S Feferman 1985],[Carvallo ,M.1968],[Conway J.H.1976],[Mesenqeur J.1989])

Remark 32. We remind to you that by the extended Stone's representation theorem for any distributive lattice we get as a corollary that:

Every partially ordered set has a monomorphic image in a lattice of sets (relative to inclusion ).

Every partially ordered set has a monomorphic image in the full binary tree.

This is a very useful result that is not mentioned widely.

It can be also considered as an extension of the Stone's representation theorem, in two directions: a) to every (partially)ordered set b) the representation is not order-isomorphism but order-monomorphism (isotonous mapping ).

About its proof: As it is known, it holds a "linearisation" theorem for any (partially) ordered set :Every (partially) ordered set has an order-monomorphic image in an order type .The order types are distributive lattices. Thus by the extended Stone's representation theorem every (partially) ordered set has an order-monomorphic image in a lattice (relative to inclusion) of sets.

About the second assertion: The lattice of sets that was mentioned in the previous assertion is a Boolean lattice of the type. The lattice direct-product ordering of it has by the identity mapping an order-monomorphic image in the set ={0,1}^α and in the lexicographic ordering; where the a is the cardinality of X, thus an initial ordinal number.

The {0,1}^α is a level of the full binary tree D_α of height a.

The ordering of the level can be taken to be the lexicographical ordering Q.E.D.

Acknowledgments. I would like to thank professor Kirby Baker (Mathematics Department of the UCLA) for the interest that he showed for the λ-rainbow lattices and his valuable remarks.

Also professor G.Moschovakis (Mathematics Department of the UCLA) for giving to me the opportunity to visit the Mathematics Department of the UCLA.

Bibliography

Abbot, J.C. 1969	Sets, Lattices, and Boolean Algebras, Allyn and Bacon, 1969.
A.I. Appudia, N.C.A., Da Costa R. Ghuaqui 1977	Non-classical Logics, Model Theory and Computability North-Holland 1977.
J. Barwise, S. Feferman 1985	Model Theoretic Logics especially chapter II Extended Logics by H-D Ebbingaus Springer 1985.
Birkhoff, G. 1967	Lattice theory Amer. Math. Soc. Coll. Publ., Vol., XXV, Providence, 1967.
Birkhoff, G. – MacLane, S. 1977	A survey of Modern Algebra. Macmillan Pub, C. 4-eddition 1977.
Birkhoff G. – v. Neumann, J. 1936	The logic of Quantum Mechanics. Annals of Mathematics 37, pp 823-843 (1936) reprinted in J, v. Neumann Collected Works vol. 4 pp 105-125.
Carvallo, M. 1968	Logique à trios valeures logique à seuil Collection de Mathematiques Economiques Gauthier-Villars Paris 1968.
Cohn P.M. 1965	Universal Algebra Harper-Row-Weatherhill P.C. 1965.
Conway J.H. 1976	On numbers and games. Academic press 1976.
H-D Ebbinghaus J. Flum W. Thomas 1984	Mathematic Logic Springer 1984.
L. Fuchs 1963	Partially ordered Algebraic Systems Addison-Wesley Pergamon press 1963.
Glayzal A. 1937	Transfinite real numbers Proc of the Nat. Acad of scien. 23 (1937) pp 581-587).
Grätzer, G. 1978	General Lattice Theory, Academic Press, 1978.
Grätzer, G. 1979	Universal Algebra Springer V. 1979.
Lukasiewicz, J. 1920	O logice trojwartisciowej (on three-valued logic) Ruch Filozoficzny 5, (1920) pp 169-171 reprinted in J. Lukasiewicz, Selected Works L. Borkowski North-Holland Pub.C. 1970 pp 87-88.
MacLane S. 1971	Categories for the Working Mathematician. Springer V. 1971.
Neumann B.H. 1949	On ordered division rings Transactions of the A.M.S. 60 (1949) pp 202-252.
von Neumann, J. 1960	Continuous Geometry Princeton University Press 1960.
Piron Constantin 1964	Axiomatique Quantique Helvetica Physica Acta 37 (1964) pp 439-468.
Post, E.L. 1921	Introduction to a general theory of elementary propositions Amer. J. Math, vol. 43, (1921) pp 163-185.
Putnam, H. 1957	Three-valued logic Philosophical studies 8. (1957) pp 73-80.
Rasiowa Helena 1974	An Algebraic Approach to non-classical Logics. North-Holland 1974.
Rieger Ladislav 1967	Algebraic methods of mathematic Logic. Academic 1967.
Robinson A. 1966	Non-standard Analysis North-Holland 1974 (1966).
Rosser J.B.-Turkuette, A.R. 1952	Many-Valued Logic North-Holland Publ, C. 1952.
Manin Y.I. 1977	A course in Mathematical Logic. Springer 1977.
J. Mesequer 1989	General Logics In the "Logic Colloquium 1987" Studies in Logic v. 129 North Holland 1989.
Sikorski, R. 1969	Boolean Algebras Springer Verlag, 1969.
Springer Publications 1987	Ω-bibliography in Mathematic Logic vol I: Classical Logics vol II: Non-classical Logics vol III : Model Theory vol IV: Proof Theory constructive mathematics.
v. Weizsäcker C.F.-Sheibe, E. Sûssmann G. 1958	Koplementarität und Logik Zeitschrift für Naturforschung 13 a, pp 705-721 (1958).
Zadeth, L.A. 1965	Fuzzy sets Information and Control 8, 338-353 (1965).

Key Words

Lattices,

general logic

Boolean lattices, logic

Postean lattices, logic

Fuzzy-subsets lattices, logic

transfinite real numbers

Note on the relation of the Fuzzy subsets, Postean,

Boolean lattices. The λ-rainbow lattices.

The transfinite (real, complex, quaternion) Fuzzy subsets.

By Dr Constantine E. Kyritsis

Abstract

In this short note the main results are:

1) They are introduced axiomatically the λ-rainbow lattices. It is proved that the λ-Fuzzy subsets lattices are distributive λ-rainbow lattices and other relations of these two classes of lattices.

2) They are introduced the transfinite real, complex, quaternion. Fuzzy subsets. They can be considered as a kind of Arithmetisation of the abstract λ-Fuzzy subsets lattices. The transfinite real Fuzzy subsets are special λ-Fuzzy subsets with good properties.

3) It is proved a mutual isomorphic representation of the Boolean (2-valued logic) Postean (3-valued logic) and Fuzzy-subsets (Fuzzy-logic) lattices.

extremes 0,1 of the lattice. We define the function: by h(x)=a_x where a_x (t) = .

We shall prove that the h is a lattice isomorphism of L and its range .

a) We shall prove that h (xÙy)=h(x)Ùh(y). Let h(x)=a_x and h(y)=a_y.

Let us suppose that xÏt and yÏt for some tÎ SpecL. Then a_x=1=a_y. If xÙyÎt and because the t isa prime ideal we deduce that either xÎt or yÎt, contradiction. Thus xÙyÏt, hence a_xÙy=1 and a_xÙy=1=1Ù1=a_xÙa_y. The other case is that either xÎt or yÎt. Then either a_x=0 or a_y=0. In both cases, because the t is an ideal xÙyÎt and thus a_xÙy=0; and a_xÙy=0=0Ù(0 or 1) = a_xÙa_y.

b) We shall prove that h(xvy)=h(x)vh(y). Let us suppose that xÎt and yÎt for some tÎSpecL. Then a_x(t)=1=a_y(t). If xvyÎ and because the t is an ideal we deduce that x, yÎt, which is a contradiction.

Thus xvyÎt and a_xva_y=1. Thus a_xvy (t)=1=1v1=a_x (t)va_y(t). The other case is that either xÎt or yÎt. Then either a_x(t)=o or a_y(t)=0. And if xvyÎt then because the t is an ideal we deduce that x,yÎt thus a_xvy(t)=0=0v0=a_x(t)va_y(t). If xvyÎt, then either xÎt or yÎt (in the contrary xvyÎt which is a contradiction). Thus either xÎt and yÎt or xÎt and yÎt. In both cases a_xvy(t)=1=1v0=0v1=a_x(t)va_y(t).

c) We shall prove that if x¹y then h(x)¹h(y).

If x¹y because the SpecL is separating there is tÎSpecL such that xÎt and y¹t. Thus a_x(t)=0 and a_y(t)=1 hence a_x¹a_y or h(x)¹h(y). By the a), b), c) we conclude that the h is a monomorphism of the lattices L and h(L)£ . But in the category of lattices a monomorphism and epimorphism is also an isomorphism

Q.E.D.

Corollary 21. (The extended Birkhoff-Stone theorem).

A lattice is with separating spectrum if and only if it is distributive.

Proof: By the Birkhoff-Stone theorem we get that any distributive lattice is with separating spectrum. By the extended Stone’s theorem 20 we get that any lattice with separating spectrum is isomorphic with a sublattice of a Boolean lattice. But any sublattice of a Boolean lattice is a distributive lattice.

Q.E.D.

Remark: We conclude that any distributive lattice has a representation with sets: This seems that it is already known (see [Sirkoski,R 1969] Appendix §3 first page of the paragraph). Our proof does not nevertheless make use of any distributive assumption for the lattice. With our technique it is proved something more: The inverse of the Birkhoff-Stone theorem.