ORDINAL REAL NUMBER 3. The
techniques of transfinite real , surreal,
ordinal real, numbers ; unification .
By Dr. Constantine E.
Kyritsis
Department of Mathematics
and Computer Science
Software Laboratory
Electrical and Computer Engineering
http://www.softlab.ntua.gr/~kyritsis
§ 0 Introduction . In this third paper on
ordinal real numbers, it is proved that the three different techniques and Hierarchies of
transfinite real number-fields, of surreal numbers, and of ordinal real numbers
, give by inductive limit ,or union, the same class of numbers ,already known
as the class No .It can be characterized, simply, as the smallest (linearly
ordered field which is a ) class and
contains every linearly ordered set- field as a subfield . Ôhis class ,and also the category of linearly ordered
set-fields, we call " the linearly ordered Newton-Leibniz
realm of numbers". It is obvious that without the set theory of G. Cantor
as it is formalized, for instance, by Zermelo-Frankel and a correct thinking about the infinite,
this "realm of numbers"
would not be definable.
Nevertheless
we could follow a still different approach. If in the completion of rational numbers to real numbers we ramify
the equivalence relation of convergent sequences to others that include not only where the sequences converge (if they converge at the same point)
but also how fast (if they converge in the same way e.g finally equal ,an attribute
related also to computer algorithms complexity)
,then we get non-linearly ordered topological fields that contain
ordinal numbers (certainly up to ùa , a= ùù)
and are closer to practical applications. This approach does not involve the random variables at all, but involves
directly sequences of rational numbers as "Newtonian fluxions". This creation can be
considered as a model of such linearly ordered fields
(up-to-characteristic ùa , a= ùù)
,when these linearly ordered fields are defined axiomatically. This gives also
a construction of the real numbers with a set which is countable. This does not
contradict that all models of the real numbers are isomorphic as the field-
isomorphism is not in this case also an Î-isomorphism so the Cauchy-real numbers and such a model still have
different cardinality.
If we want to define in this
way all the Ordinal real numbers , then it is still possible but then
this would give also a device for a model of all the ZFC-set theory! And such a
model is indeed possible: By taking again sequences of non-decreasing (in the
inclusion) finite sets of ZFC , and requiring that any property ,relation
or operation if it is to hold for this set-sequence it must hold finally for
each term of the sequence and finite set. In other words we take a minimality for
every set of it, relative to the axiom of infinite. It is easy to prove that
the (absolute) cardinality of such a model is at most 2ù ,
that is at most the cardinality of the continuum. We could conceive such
a model as the way a computer with its algorithms , data bases tables etc
would represents sets of ZFC in a logically consistent way. Needles to say that
a similar model of ZFC set theory could be given within Euclidean geometry!
(e.g. after the Hilbert's axiom system, and in addition accepting only the
natural numbers). There
is no contradiction with the 2nd-incompletness theorem of Gödel as the
argument to prove that it is a model of ZFC-set theory is already outside
ZFC-set theory (as are also the arguments of Gödel ,or of
Lowenheim-Skolem that gives a countable
model of ZFC-set theory).
It is not
directly apparent that so different techniques
and ideas would have
such an underlying unity.
It is, also , surprising
that, although the Hessenberg operations were
very early known in the theory of ordinal numbers, (at least since 1906, see [ Gleyzal A. 1937]) no one went far enough to define through them, fields in a
way similar to the way that the real
numbers are defined from the natural numbers.
Although G.Cantor, himself
was conceiving the ordinals as a natural continuation
of the
natural numbers (see [Frankell
A. A. 1953 ] introduction pp 3 ) ,as
it is kmown,
he rejected the attempts to
define infinitesimals through
them . (see [Frankell A. A. 1953]
ch ii § 7.7 pp 120). We could speculate
that un underlying reason for
this, might be that,
his set-theory was
already strongly attacked and
was facing the
danger of final rejection ,and these were good enough reasons to avoid
the additional charge that
his theory "
opened the door"
to infinitesimals . In spite of this, there are many who might consider that although the present results
are coming now, nevertheless it is too late and ,they might speculate ,for this
long delay (more
than eighty years) and
diversion of ideas and technique,
nevertheless on the same
subject, we could
suspect systematic
obstructions, that came outside
the mathematics. Nevertheless,
there are others who consider that it is too
early for such a development ,and especially for an
analysis on such numbers. It seems that it has never been published any "partially ordered Newton-Leibniz
realm of numbers" (in other words a category of transcendental
extensions of the real numbers ,that are partially ordered fields and complete in the order topology
) with reasonably "good" properties for a
classification. In this paper we use the surreal numbers, as they are
definable in the Zermelo-Frankel set theory, through the binary trees, directly
as a class, and not as union of some set fields.(The original technique of
J.H.Conway).I met J.H.Conway during 1992 at Philadelphia in the USA, I talked
to him about the new developments in this area of research and I gave to him
the present work but as he told me he had more than a decade that for the last
time he had active interest in the subject. I is somehow necessary to make use
of classes instead of sets; since, for the kind of "induction" that
the J.H.Conway uses, we prove that it is
reduced to the usual transfinite induction on the height of the elements of the
trees; but in their union as a class and not for each one of them
separately as a set; in the latter case in
which the trees
are sets the induction
fails .The key-point is to prove that for every cut that J.H.Conway uses
it does really exist a unique element of the trees of least
height . "simplest number" as it is used to be called ). This is
a very crucial point, for the whole
technique of the surreal numbers,
to work, and it
seems that it
has been obscured, by not
paying sufficient attention to it
The author has initially included also the
non-standard real numbers in the classification. As they are also linearly
ordered fields and the present classification is of all linearly ordered fields
it was natural to include them. There were experts in non-standard analysis
that were glad about it. Nevertheless there were experts that insisted that
according to the initial definition of A.Robinson and not of later definitions,
it was not claimed that the non-standard real numbers were sets inside
Zermelo-Frankel system. Only if Zermelo-Frankel system was used to model
meta-mathematics also the they would be also sets. This was nevertheless
different as such sets would models of meta-mathematical entities different
than the sets that are models of mathematical and not meta-mathematical
entities. Because of their arguments and in spite the fact that this made some
other researchers of non-standard mathematics unhappy, the author prefers in
this first publication about ordinal real numbers not to include the
non-standard real numbers in the unification. Any definition nevertheless that
has the non-standard real numbers as ordinary sets of Zermelo-Frankel set
theory, would naturally lead to a straightforward proof that such fields are always
subfields of some field of ordinal real numbers! The author has already
produced pages with this proof that is based on the premise that I mentioned.
§ 2. The
surreal numbers .
In this
paragraph we define the class No of surreal numbers inside the ZF-set theory.We
use the binary trees (see [
Conway J.H. 1976] appendix to part zero pp 65
and [Kuratwski K.-Mostowski A.
1968] Ch
IX §1, §2).The crucial point is to prove that for
the cuts defined by J.H.Conway in these trees it does really exist a unique
element strictly greater than all the elements of the left section and strictly
smaller than all the
elements of the
right section (the "simplest
number" ).Through this the Conway-induction us reduced to the usual
transfinite induction on the height of the elements of the tree .As we shall
see this works for the union of all trees as a class but fails for each one
set-tree .For the definition of the
tree, binary tree, height, levels of the tree ,Hî-set see
[Kuratwski K.-Mostowski A. 1968]
Ch IX §1, §2 Theorem 2, . The binary tree of height
á we denote by Dá . More precisely we are interested for the trees of the next
definition.
Definition
1. Let
á be an ordinal . We define ![]() = {x|x
= {x|x ![]() Da such that
there is â<á such that
for the
element x as a zero-one sequence x = {xî|î<a} holds that xâ = 1 and xî = 0 for î>â}.
Da such that
there is â<á such that
for the
element x as a zero-one sequence x = {xî|î<a} holds that xâ = 1 and xî = 0 for î>â}.
We call the set ![]() the open full-binary tree of height á.
the open full-binary tree of height á.
We also remind that if for the height á, holds that À(á) is a
cofinal to á regular aleph: À(á) = Àcf(á)= Àî the open full-binary tree is an Hî set, (see
[Kuratwski K.-Mostowski A. 1968] ChIX §2 Theorem 2, the proof works also
for trees ![]() where À(á)= Àcf(á))
where À(á)= Àcf(á))
Lemma 2.
For every pair
of subsets L,
R of the open-full-binary tree ![]() of height
the ordinal á, such that À(á) is a regular aleph, and holds that: for every l
of height
the ordinal á, such that À(á) is a regular aleph, and holds that: for every l![]() L, r
L, r![]() R, l < r, and À(L), À(R) < À(á), there is
exactly one element x0
of least height in
R, l < r, and À(L), À(R) < À(á), there is
exactly one element x0
of least height in ![]() such that l
< x0 <
r for every l
such that l
< x0 <
r for every l ![]() L, r
L, r ![]() R.
R.
Proof. Let D(L) = {x|x ![]()
![]() such that there exists l
such that there exists l ![]() L with x £ l} and I(R) = {x|x
L with x £ l} and I(R) = {x|x ![]()
![]() such that there exists r
such that there exists r ![]() R with r
R with r ![]() x} that is D(L), I(R) are the decreasing and
increasing lower and upper half subsets of
x} that is D(L), I(R) are the decreasing and
increasing lower and upper half subsets of ![]() determined by L, R, in the linear ordering of
determined by L, R, in the linear ordering of ![]() as a tree (see [Kuratwski K.-Mostowski A.
1968] Ch IX §1 Lemma A). Let the set M =
{x|x e
as a tree (see [Kuratwski K.-Mostowski A.
1968] Ch IX §1 Lemma A). Let the set M =
{x|x e ![]() and for every Ë l
and for every Ë l ![]() D(L), r
D(L), r ![]() I(R) it holds that l < x < r}. By the Hî property of
I(R) it holds that l < x < r}. By the Hî property of ![]() it
holds that M ¹ Æ . Let A = {â|â is an ordinal number such that there is x
it
holds that M ¹ Æ . Let A = {â|â is an ordinal number such that there is x ![]() M with x
M with x ![]() Tâ where Tâ is the â-level of Dá in other words there is x
Tâ where Tâ is the â-level of Dá in other words there is x ![]() M of height â}. Let á0 = min A. Let
Dá0(L) Iá0(R) the subsets of D(L) R(L) of elements of
height less than á0, and let Má0 Í M the subset of M that consists of elements of height á0. Suppose
that the set Má0 contains two elements x, y with e.g. x £ y. We will prove that Má0 contains only one element.
M of height â}. Let á0 = min A. Let
Dá0(L) Iá0(R) the subsets of D(L) R(L) of elements of
height less than á0, and let Má0 Í M the subset of M that consists of elements of height á0. Suppose
that the set Má0 contains two elements x, y with e.g. x £ y. We will prove that Má0 contains only one element.
Let
x'={xâ|â<á0} that is that part of the á0-sequence x with terms of indifes less than á0. And
the same
also with y' = {yâ|â < á0}. Then
there is
lx or rx
and ly or ry
respectively in Dá0(L), Iá0(R) such that they are equal with x', y'. If x=rx then, if the á0-term of x
is 0 or 1, in both cases x > rx,
contradiction. Hence there is no
such rx and also such ry. Then lx=x'
ly=y' and lx£ly. The á0-term of x
and y might be 0 or 1. The only possible
cases are {x =
(lx,0), y = (ly,0)}, {x = (lx,0), y = (ly,1}
{x = (lx,1), (ly,1)}, {x = (lx,1), y = (ly,0}
where with the parenthesis we symbolize the á0- sequence
which is the elements x, y. Let us suppose that x ¹ y and ![]() , the
part of the á0-sequence with terms with indices less than ä, with ä £ á . Let the least value of ä, be denoted
by ä0 such
that
, the
part of the á0-sequence with terms with indices less than ä, with ä £ á . Let the least value of ä, be denoted
by ä0 such
that ![]() . If holds that
. If holds that ![]() because x<y. In the sequent, let z=(Dâ(x)=Dâ(y) â< ä0, 1). Then x < z £ y. If ä0 = a0 then x=y because Xá0 = Yá0 = 1. Then ä0 < á0 and also z
< y and x < z< y and the height of z is ä0 < a0
contradiction. Hence x=
y, and Má0 contains only one
element. It also holds that if we
restrict to Dc(L), Ic(R) where
because x<y. In the sequent, let z=(Dâ(x)=Dâ(y) â< ä0, 1). Then x < z £ y. If ä0 = a0 then x=y because Xá0 = Yá0 = 1. Then ä0 < á0 and also z
< y and x < z< y and the height of z is ä0 < a0
contradiction. Hence x=
y, and Má0 contains only one
element. It also holds that if we
restrict to Dc(L), Ic(R) where ![]() (and L, R have height <c), then a0
£ c by the Hî-property of
(and L, R have height <c), then a0
£ c by the Hî-property of ![]() if c is
also such that À(á)= Àcf(á) q.e.d.
if c is
also such that À(á)= Àcf(á) q.e.d.
Definition
3. The
open full binary tree ![]() of height á, such that À(á) is a cofinal to á, regular
aleph , I call regular open full- binary tree.
of height á, such that À(á) is a cofinal to á, regular
aleph , I call regular open full- binary tree.
The property of the previous lemma of a regular open
full-binary tree I call Hî-leveled Dedekind completness.
We remark that the class of regular alephs is
unbounded (see [Kuratwski K.-Mostowski A. 1968] p. 275 relation 5 ) Thus the
class of ordinals á such that À(á)= Àcf(á) is unbounded.
The next definition is the definition of the class of
surreal numbers in the ZF-set theory and it depends as we mentioned on the
lemma 2 .As it is seen ,in the
hypotheses of the lemma 2 the cardinality of halfs of the
cut is bounded by À(á). If it is to include all
possible cuts of the tree ![]() then the lemma 2 will give the element xï in some tree
then the lemma 2 will give the element xï in some tree ![]() , of sufficient
greater height,thus outside
the original tree Dá. This is why
we mentioned that
the definition of surreal numbers (with the original technique of
J.H.Conway ) does not apply to the trees
, of sufficient
greater height,thus outside
the original tree Dá. This is why
we mentioned that
the definition of surreal numbers (with the original technique of
J.H.Conway ) does not apply to the trees ![]() separately .
separately .
Definition
4. Let U![]() =No be the union of all regular open full-binary trees. It is a class (after
axiom A2.(see [Cohn P.M. 1965] p1-36)) Operations may be defined in this
linearly ordered class according to the
formulae of Lemma 2 in [Kyritsis C.1991 Alt. or Free etc.)] II, that hold for
every linearly ordered field that is:
=No be the union of all regular open full-binary trees. It is a class (after
axiom A2.(see [Cohn P.M. 1965] p1-36)) Operations may be defined in this
linearly ordered class according to the
formulae of Lemma 2 in [Kyritsis C.1991 Alt. or Free etc.)] II, that hold for
every linearly ordered field that is:
1. let á be an ordinal with À(á)= Àcf(á) and L,R
subsets of ![]() such that for every l Î L, r Î R holds that l < r. Then there exists a regular
aleph â such that
such that for every l Î L, r Î R holds that l < r. Then there exists a regular
aleph â such that ![]() and À(L), À(R)< À(â). Then
there is by lemma 2 a unique element
and À(L), À(R)< À(â). Then
there is by lemma 2 a unique element ![]() of least height such that l < x0 < r for
every l Î L, r Î R, we
denote this element by {L|R} and
we write x0= {L|R}. We
note that although
of least height such that l < x0 < r for
every l Î L, r Î R, we
denote this element by {L|R} and
we write x0= {L|R}. We
note that although
![]() , it holds that
, it holds that ![]() and á <â.
and á <â.
2. If ![]() and we denote the height of x, y by h(x), h(y) and by L(x), L(y), R(x), R(y) the
sets
and we denote the height of x, y by h(x), h(y) and by L(x), L(y), R(x), R(y) the
sets
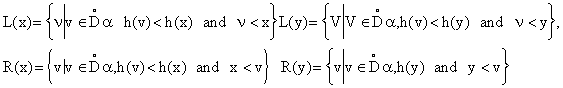 Then the operations are defined through simultaneous two-variable transfinite induction in the form of the
lemma 2,3 in [ Kyritsis C. 1991 Free etc.], for
the heights of the trees
Then the operations are defined through simultaneous two-variable transfinite induction in the form of the
lemma 2,3 in [ Kyritsis C. 1991 Free etc.], for
the heights of the trees ![]() where for the initial segments of
ordinals we substitute the corresponding
trees of No (For every ordinal â<á such that N(â)=Ncf(â) corresponds a tree
where for the initial segments of
ordinals we substitute the corresponding
trees of No (For every ordinal â<á such that N(â)=Ncf(â) corresponds a tree ![]() ). Thus
the function of operation is defined not
on w(á)2
but on
). Thus
the function of operation is defined not
on w(á)2
but on ![]() 2. For the addition, the next rule
is used x+y={L(x)+y È x+L(y)| x+R(y)} È R(x)+y}.
2. For the addition, the next rule
is used x+y={L(x)+y È x+L(y)| x+R(y)} È R(x)+y}.
3. The opposite
is defined by:
-x = {-R(x)|-L(x)}
4. Multiplication is defined by
x.y={L(x).y+xL(y)-L(x).L(y)ÈR(x).y+xR(y)-R(x)R(y)½
|L(x).y+x.R(y)-L(x).R(y) È R(x).y+x.L(x)-R(x).L(x)}.
This
definition presupposes the definition of addition.
5. Inverse is defined by
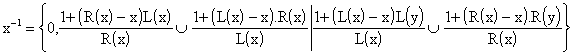
As it is proved
in [Conway J.H. 1976] Ch0, 1 the set No is a linearly ordered c-field. The
characteristic of No is easily proved to
be Ù1, we call
this c-field, c-field of surreal numbers. According to Definition 3 No is an Hî -leveled Dedekind
complete field.
§ 3 The unification .
In this
paragraph we prove
that all the
three different techniques and
hierarchies of transfinite real ,of surreal ,of ordinal real numbers give by inductive limit or union the same
class of numbers .We
have already proved
that CR=Ù1R=C*R. (see corollary 10) and it remains to
prove No=CR.
Lemma 5 . It holds that
CR=Ù1R=C*RÍ No.
Proof .Let an
open full binary
tree ![]() of
height the principal ordinal a .Then
of
height the principal ordinal a .Then
![]() Í No ,and the
field-inherited operations in the initial segment
W(á) are
the Hessenberg operations (see
[Conway J.H. 1976] ch 2 § ""containment of the ordinals "note pp
28 and also [Kyritsis C.1991 Alt] the characterisation theorem ).If á was not a principal ordinal, the W(á) would not be closed to the Hessenberg operations .Thus the Ná, Zá, Qá are contained in No ,since what it is used to define
them from W(á) is only the field operations
.The Qá is a field
and from the fact that No is closed
to extensions of its
set-subfields (see[ Conway J.H. 1976] ch
4 theorem 28
)we deduce that
the field of ordinal real numbers
Rá is
contained in No, for
every principal ordinal number á .Thus ÈRá=Ù1RÍNo .Q.E.D.
Í No ,and the
field-inherited operations in the initial segment
W(á) are
the Hessenberg operations (see
[Conway J.H. 1976] ch 2 § ""containment of the ordinals "note pp
28 and also [Kyritsis C.1991 Alt] the characterisation theorem ).If á was not a principal ordinal, the W(á) would not be closed to the Hessenberg operations .Thus the Ná, Zá, Qá are contained in No ,since what it is used to define
them from W(á) is only the field operations
.The Qá is a field
and from the fact that No is closed
to extensions of its
set-subfields (see[ Conway J.H. 1976] ch
4 theorem 28
)we deduce that
the field of ordinal real numbers
Rá is
contained in No, for
every principal ordinal number á .Thus ÈRá=Ù1RÍNo .Q.E.D.
Lemma 6 . For every
regular open full binary tree ![]() , it holds
that
, it holds
that ![]() Í Râ, for some
sufficiently big principal ordinal number â . (With the inclusion is meant that the restriction
of ordering of Rá in the
tree, coincides with the ordering of the tree).
Í Râ, for some
sufficiently big principal ordinal number â . (With the inclusion is meant that the restriction
of ordering of Rá in the
tree, coincides with the ordering of the tree).
Proof . We shall prove it by transfinite induction .It
holds for the trees of finite height. The
transfinite induction shall be on the transfinite sequence of all ordinal
numbers such that À(á)= Àcf(á) and À(á) is a
regular aleph. Let us suppose that it holds for all such ordinal numbers of W(á), and À(á)= Àcf(á) and À(á) is a
regular aleph .Then : ![]() where â(á) is a
principal ordinal with
where â(á) is a
principal ordinal with ![]() . q.e.d.
. q.e.d.
From the previous lemma we get that È![]() = No Í Ù1R ,thus :
= No Í Ù1R ,thus :
The
unification theorem 7
It holds
that the classes of transfinite real numbers CR , of surreal numbers No, of
ordinal real numbers Ù1R ,coincide ,and it is the smallest class (and
linearly ordered c-field ) ,that
contains all linearly ordered set-fields as subfields.
We can have
obviously analogous
statements for the
other classes of numbers (complex
, quaternion e.t.c.). After the previous theorem, the binary arithnetisation of
the order-types, stated in [ Kyritsis C. 1991] II
,theorem 11, is directly provable. We remark that because
the levels of the open full binary trees have the property that any upper
(lower bounded set has supremum (infimum ) ,(see [Kuratowski K. -Mostowski A 1968] ch ix §1, § 2 theorem 2 ),and after the Hilbert and
fundamental (Cauchy) completness of the ordinal real numbers, and remark
after definition 13 and ù-normal form according to [ Frankel A.A. 1953] ch 3 theorem 21 ,and after corollary 21 in [Kyritsis C. 1991] ,II
, we also get:
Theorem 8 . The class of
numbers CR=Ù1R=No has
leveled formal power series
representation, leveled Hilbert completeness, leveled fundamental
(Cauchy) completeness, leveled Hî Dedekind
completeness ,leveled supremum completeness and representation with ù-normal forms.
Bibliography
[N.
L. Alling 1987] Foundations
of analysis over surreal number fields North-Holland Math.Studies V. 141 1987 .
[
Artin E.
Schreier O.1927] Algebraishe konstruktion reellerkorper, Abh. Math.
Sem.Univ.
[
Artin E. - Tate J.1967 ] Class
Field Theory Benjamin 1967.
[Baer Reinold,1970] Dichte,Archimedizitat und Starrheit geordneter Korper,
Mathematische Annalen 188 pp 165-205, 1970.
[Baker
Alan1975 ]
[ Bourbaki N.1952] Elemente de Mathematique algebre, chapitre III Hermann Paris 1948, chapitre VI
Hermann Paris 1952.
[Brown
Ron 1971 ] Real places and Ordered Fields Rocky
Mountain Journal of Mathematics , Vol 1 ,pp 633-636, 1971.
[Brown
R.,Craven T.C., Ordered fields
satisfying Rolle's Theorem.
Pelling M.J.1986]
[Clliford A. H.1954] Note on
Hahn's theorem on ordered
abelian groups. Proc. of the Amer. Math. Soc. 5 (1954) pp 860-863.
[Cohen L.W.-
Goffman C.1949] Theory
of transfinite
Convergence.Transact. of the Amer. Math. Soc. 66 (1949) pp 65-74.
[Cohn
P.M.1965] Universal Algebva Harper - Row 1965 .
[
[Cuesta Dutardi
N.1954] Algebra Ordinal Rev. Acad. Cientis
[Dugundji
J.1966] Topology, Allyn and Bacon
inc. 1966.
[Ehreshmann
Ch.1956] Categories et structure Dunod 1956
[Ehrlich
P.1988] An alternative construction of
[Ehrlich
P.] The
Dedekind completion of No ,submitted to Algebra Universalis.
[Endler O.1972] Valuation
Theory, Springer 1972.
[Erdos
P.-Gillman L.- An isomorphism theorem for real
closed fields
Henrkiksen
M..1955] Ann. of
Math.(2) 61 (1955)pp 542-554.
[Frankel
A.A.1953] Abstract set
Theory. North -
[Fuchs
L.1963 ] Partially ordered algebraic systems
Pergamon
[Gillman
L.-Jerison M.1960] Rings of continuous functions.Van Nostrand
Princeton 1960.
[Gleyzal
A.1937] Transfinite real numbers. Proc. of
the Nat. Acad.of scien. 23 (1937) pp 581-587.
[Gravett
K.A.H.1956] Ordered abelian groups. Quart. J.
Math.
[Hahn
H. 1907] Uber die nichtarhimedishen
Grossensysteme.S. Ber. Akad. Wiss. Wein.
Math. Natur.Wkl Abt. IIa 116
(1907) pp 601-655.
[Hausner
M.-Wendel J.G.1952] Ordered Vector Spases Proc. of the
Amer. Math. Soc.3 (1952) pp 977-982.
[Hessenberg
G.1906] Grundbegriffe der
Mengenlehre (Abh. der
[Hilbert
D.1977] Grundlagen der Geometry Teubner
Studienbucher 1977 .
[Hilbert
D. -Ackermann W.1950] Principles of Mathematical Logic. Chelsea Pub.
[Kaplansky
I.1942] Maximal fields with valuations Duke
Math. J. 9 (1942) pp 303-321.
[Krull
W.1931] Allgemeine
Bewertungs theorie. J.reine angew. Math. 176 (1931) pp 160-196.
[Kuratowski
K.1966] Topology v.I
v.II Academic Press 1966.
[Kuratowski
K. -Mostowski A.1968] Set Theory
North -
.
.
[ Kyritsis C.E.1991] Algebraic characterisation of the Hessenberg operations in
the ordinal numbers. (unpublished yet).
[
Kyritsis C.E.1991] Ordinal real numbers 1. The ordinal
characteristic.(unpublished yet ).
[Lang
S.1984] Algebra . Addison-Wesley P.C. 1984 .
[Lam
T.Y.1980] The Theory of Ordered Fields Ring
theory and Algebra III. Edited by B.R.
McDonald Dekker 1980 pp 1-268.
[Laugwitz
Detler 1983] Ù Calculus as a
Generalization of Field Extension. An
alternative approach to non-Standard analysis "Recent developments in non-standard analysis" Lecture Notes in
Math 983 Springer 1983.
[MacLane S.1939] The Universality of Formal Power Series fields.Bull. of the
Amer. Math. Soc. 45 (1939) pp 880-890.
[MacLane
S. 1971] Categories for the working
mathematician Springer 1971
[Massaza
,Carla1970] On the completion of ordered fields .
Practica (=Proceedings) of the
[Monna
A.F.1975] Analyse non-Archimedienne Springer
1970.
[Munkress
J.R.1975] Topology. Prenctice Hall 1975.
[Nachbin L.1976] Topology and
Order. Robert E.Krieger P.C.
N.Y. 1976.
[Neubrunnova
Anna1980] On transfinite convergence and generalised
continuity. Mathematica Slovaca vol 30,1, 1980.
[Neumann
B.H.1949] On ordered division rings. Transact. of
the Amer. Math. Soc. 66 (1949) pp 202-252.
.
[Prestel
Alexander1980] Lectures on formaly real fields .Lecture
Notes 1093, Springer ,1980 .
[Robinson
A.1966] Non-Standard analysis.North-Holland
1974 (1966).
[Robinson
A.1972] On the real Closure of a Hardy Field.
pp 427-433 in the Theory of Sets and topology. A Collection of papers in honour
of Felix Hausdorff , VEB ,1972 .
[Rolland,Raymond
.1981] Etudes des courpure dans les groupes et corps
ordonnes. Dans Geometrie Algebrique Reeles et Formes Quadradiques.
[Rudin
W.1960] Fourier analysis on groups. Interscience
Pub 1960 .
[Shilling
O.F.G.1950] The theory of valuastions.Amer. Math.
Soc. 1950.
[Schubert H.1972 ] Categories
Springer 1972.
[Scott,
Dana 1969,] On Completing Ordered Fields. In
Applications of Model theory to Algebra, Analysis and Probability edited by
W.A.J. Luxenburg pp 274- 278,Holt
Rinehart and Winston 1969.
[Sirkoski
R. 1948] On an ordered algebraic field.
Warsow, Towarzytwo Nankowe Warzawskie 41 (1948) pp 69-96.
[Stone
A.L.1969] Non-Standard analysis in topological algebra in Applications of Model
Theory to Algebra, Analysis and Probability
N.Y. (1969) PP 285-300.
[Stroyan,
K.D. and Introduction to the theory
of Infinitecimals
Luxenburg W.A.J.1976] N.Y.1976.
[Lynn
A.Steen- Counterexamples in
Toplogy Springer 1970 .
Seebach J.A. Jr.1970]
[Viswanathan
T.M.1977] Ordered fields and sign-changing
polynomials. Journal fur reine und angewante Mathematik, 296 pp 1-9,1977.
[Van
der Waerden B.L.1970] Algebra V1
V2 Frederick Unger Pub.
[Weil
A.1967 ] Basic Number Theory,
Springer Verlag
[Zakon
E.1955] Fractions of
ordinal numbers Israel Institute of Tecnology Scient. Public. 6, 94-103
1955.
[Zariski
O. -Samuel P.1958] Commutative Algebra
V.I.II Springer 1958.
[Zervos,S.P.1961] Sur
les rapportes entre la completions la
cloture algebrique des corps commutatifs de caracteristique zero C.R. Acad. Sc.
Paris, 5 Avril 1961 t. 282 pp 2053-2055.
[Zervos,S.P.1991] Simple abstract and concrete considerations suggested by
Thue's theorem. Mathematics revisited, mathematicians remembered Vol.1 1991.pp
1-68.
List of special symbols
á,â,ù :
Small Greek letters
Ù1 :
Capital Greek letter omega
with the subscript 1
Fa :
Capital letter F with
superscript a.
N
: Capital Aleph ,the first letter
of the hebrew alphabet . In the text is used a capital script. letter n .
![]() : cross in a circle,
point in a circle .
: cross in a circle,
point in a circle .
Ná,Zá,Qá,Rá,: Roman capital
letters with subscript small
Greek letters
Cá,Há
*X, *R et.c :
Capital standard or roman letters with left superscript a star.
CN,CZ,CQ, :Capital standard letter c followed by
capital letters, with possibly
C*R a left superscript a star
![]() :
Capital tstandard letter with a cap.
:
Capital tstandard letter with a cap.
Ó :
Capital Greek letter sigma
![]() :
Capital standard D with subscript
a small Greek letter and in upper place a small zero.
:
Capital standard D with subscript
a small Greek letter and in upper place a small zero.
LINEAR NUMBERS 3.
The technique of
"free operations-fundamental completion" for the definition of a
well-ordered classifying Hierarchy of Linearly ordered associative commutative
number-fields. The transfinite real , the non-standard real, the
surreal numbers; unification .
by
Dr.Konstantine E.Kyritsis
Computer Technology Institute
Patra
Abstract
In this paper is
introduced a forth
new technique of
"the enlargment real numbers",that in some sense includes the
non-standard real numbers of A.Robinson.It is
proved ,that the three different
technics and hierarchies of
transfinite real numbers , of the surreal numbers
,of the ordinal
real numbers, give by
inductive limit or union the same class of numbers .
Key words
linearly ordered
commutative fields
transfinite real numbers
non-standard enlargment
fields of the real numbers
surreal numbers
formal power series fields