Full Page

ORDINAL REAL NUMBERS 1. The ordinal characteristic.

 

                                        

By Dr. Constantine E. Kyritsis

Department of Mathematics and Computer Science

University of Portsmouth

Software Laboratory

Electrical and Computer Engineering

National Technical University of Athens

http://www.softlab.ntua.gr/~kyritsis

kyritsis@softlab.ntua.gr

 

 

 

 

§0 Introduction. This is the third paper of  a series of five papers that have as goal the  definition of topological complete linearly ordered fields (continuous numbers)  that include the real numbers and are obtained from the ordinal numbers in a method analogous to the way that  Cauchy derived the real numbers from the natural numbers. We may call them linearly ordered Newton-Leibniz numbers. The author initiated and completed this  research in the island of Samos in Greece  during 1990-1992 .One years later (1993) he discovered how sequences of rational numbers with equivalent relation based not only that they converge to the same point but also with the same “speed” lead directly to a partially ordered topological complete field that is  probably nothing more that the Newtonian Fluxes.The author gave it an other name: Floware of the rational numbers . Such a field contains fields of ordinal real numbers. Seven years later (1999) he discovered how such numbers can be interpreted as fields of random variables and completions of them in appropriate stochastic limits (stochastic real numbers), that links them to applications of statistics, stochastic processes and computer procedures. Thus, for instance, the ordinal natural numbers (including w) can be interpreted appropriately as stochastic limit of normal random variables. This requires Bayesian statistics for higher ordinals. This interpretation permits stochastic differential and integral calculus that succeeds exactly where the known stochastic calculi fail!   (The known stochastic calculi are : a) that in signal theory which is based on the spectral representation of stationary processes, b) that of Ito’s usually with applications in Economics and c) that of Heiseberg-Schrondinger with applications in microphysical reality and  based on operators in Hilbert spaces) From this point of view it turns out that the ontology of infinite is the phenomenology of changes of the finite. In particular the phenomenology of stochastic changes of the finite can be formulated as ontology of the infinite .He hopes that in future papers he shall be able to present this perspective in detail. It is a wonderful perspective to try to define the Dirac’s deltas as entities of such stochastic real numbers. The present papers define the topological and algebraic structure of the ordinal real numbers and does not refer at all to their stochastic interpretation. Nevertheless as in practical applications of pre-emptive Goal Programming in Operations Research and  operating systems of computers, the non-Archimedean or lexicographic order is usually called pre-emptive prioritization order .the ordinal real numbers could as well be called (for the sake of practical applications) Linearly ordered pre-emptive real numbers .

 It is a wonderful perspective to try to define the Dirac’s deltas as natural entities of  such stochastic real numbers. If in the completion  of rational numbers to real numbers we ramify the equivalence relation of convergent sequences to others that include  not only where the sequences  converge (if they converge at the same point) but also how fast (if they converge in the same way ,an attribute related also to computer algorithms complexity)  ,then we get non-linearly ordered topological fields that contain ordinal numbers (certainly up to ùa , a=   ùù) and are closer to practical applications. This approach does not involve the random variables at all, but involves directly  sequences of rational numbers as "Newtonian fluxions". This creation can be considered as a model of such linearly ordered fields (up-to-characteristic  ùa , a=   ùù) ,when these linearly ordered fields are defined axiomatically. This gives also a construction of the real numbers with a set which is countable. This does not contradict  that all models of the real numbers are isomorphic as the field- isomorphism is not in this case also an Î-isomorphism so the Cauchy-real numbers and such a model still have different cardinality.

            If we want to define in this way all the Ordinal real numbers , then it is still possible but then this would give also a device for a model of all the ZFC-set theory! And such a model is indeed possible: By taking again sequences of non-decreasing (in the inclusion) finite sets of ZFC , and requiring that  any property ,relation or operation if it is to hold for this set-sequence it must hold finally for each term of the sequence and finite set. In other words we take a minimality relative to the axiom of infinite for every set of it. It is easy to prove that the (absolute) cardinality of such a model is at most 2ù  , that is at most the cardinality of the continuum. We could conceive  such a model as the  way a computer with its algorithms , data bases tables etc would represents sets of ZFC in a logically consistent way.There is no contradiction with the 2nd-incompletness theorem of Gödel as the argument to prove that it is a model of ZFC-set theory is already outside ZFC-set theory (as are also the arguments of Gödel ,or of Lowenheim-Skolem  that gives a countable model of ZFC-set theory).

 

 

 

 

 

 In a communication (1992) that the author had with N.L. Alling and his group of researchers on analysis on surreal numbers, suggested the term ordinal real numbers instead of surreal numbers. Some years later and before the present work appears for publication, it appeared in the bibliography conferences about real ordinal numbers .  

 

 

In these last three  papers is studied a special Hierarchy   of   transcendental   over    the    real    numbers, linearly ordered fields that are characterized by the property that they are fundamentally (Cauchy ) complete. It shall turn out  that they are isomorphic to the transfinite real numbers (see [Glayzal A. (1937)]).The author was not  familiar with the 5 pages paper of [ Glayzal A. (1937)] ,and his original term was “transfinite real numbers”. When one year later (1991) he discovered the  paper by A. Glayzal  ,he changed the term to the next closest :”Ordinal Real Numbers” .One more year later he proved that the transfinite real numbers ,the surreal numbers and the ordinal real numbers were three different techniques leading to isomorphic field of numbers. He then suggested (1992) to researchers of surreal numbers, like N.L.Alling to use the more casual term “ordinal or transfinite real numbers “ for the surreal numbers. In  the  present   work   it   is   introduced a new, better, classifying and more natural technique in order to define them. This technique I call "free  operations-fundamental  completion". It is  actually  the  same  ideas  that  lead  to  the   process   of  construction of the real numbers from the natural numbers through fundamental (Cauchy) sequenses. In the modern conceptual context of the  theory  of  categories  this  may  demand  at   least   three adjunctions (see[ MacLane S 1971 ]).It is developed their elementary  theory  which belongs to algebra. Their definition uses the Hessenberg operations of the ordinal numbers .It may be considered as making use of an infinite dimensional K-theory  which  is mainly not created yet. In this first paper it is  also  introduced the ordinal characteristic of any linearly ordered field .It is  a principal ordinal number, that is of type . These numbers ,as defined  with  the  present  technique  of  the  "free operations-fundamental completion " and prior to the proof that the resulting  linearly  ordered  fields  are  isomorphic  to  the transfinite real numbers (as in [Glayzal A. (1937)]) ,we shall call  Ordinal  real numbers. The  relevancy  with   the   surreal   numbers   and   the non-standard (hyper) real numbers ,shall  be  studied  in  a  later paper. In detail, the next  Hierarchies  are defined:

1)  The Ordinal natural numbers, denoted by  Ná .2) The  Ordinal  integral numbers, denoted by Zá 3)The  Ordinal  rational  numbers,  denoted  by Qá 4)The  Ordinal  p-adic  numbers, denoted  by  Qá,p 5)The  Ordinal  real numbers, denoted by Rá 6)The  Ordinal comlpex numbers, denoted by Cá 7)The  Ordinal quaternion numbers, denoted by Há, of characteristic á . The fields Qá,p, Rá, Cá, Há are fundamentaly (Cauchy)complete topological fields.

The   field Rá is also the   unique   maximal    field    of characteristic á ( that is, it  is  Hilbert  complete  ),  and   the unique fundamentally  (Cauchy ) complete  field  of  characteristic á. It is also a   real  closed  field  ,  according  to  the  theory  of Artin-Schreier . These will be proved in the next paper on ordinal real numbers.

As it is known there are three more techniques and Hierarchies of transcendental over the real numbers, linearly ordered fields. Namely (in the historical order): The transfinite real numbers (see [Glayzal A. 1937 ]), and the surreal numbers (see [Conway J.H (1976) ]).

In this series of papers, it is proved (among other results ) that all the previous three different techniques and Hierarchies give by inductive limit, or by union, the same class of numbers (already known as the class No ).

 

 

 

§ 1. The ordinal characteristic of linearly ordered fields.

     Definition 0. We remind the reader  that a  linearly  (totally)   ordered,  double abelian semigroup (semiring ) M  is  a  set  with  two operations denoted by +,., such that with each one of them it is an abelian semigroup. Furthermore the distribution  law holds  for multiplication over addition. A linear ordering  is supposed defined in M that satisfies  the  following compatibility conditions with the two operations 1)  if  x>y,      x'>y' x,x',y,y'M then x+x'>y+y' and xx'+yy'>xy'+yx' (The symbol < is used for £ and not equal) if M is also a monoid relative to the two  operations, and zero is  absorbent  unit for  M, M  is  called ordered double abelian monoid. (semiring)    

(e.g.The set of natural numbers ,denoted by N).

          In the next we shall consider  linearly (totally) ordered  fields.( For a definition see [Lang S.] ch xi §1 pp 391).

         Also in  the  next  we  shall  use  ordinal  numbers. (For   a reference to  standard  symbolism and   definitions   see   [Kuratowski K.-Mostowski A. 1968] ch vii, [Cohn P.M. 1965] pp 1-36 )

     In the following paragraphs  we  will  not avoid the use of larger totalities  than  the  sets  of  the Zermelo-Frankel set theory, namely classes.

          We may suppose that we work in the  Zermelo-Frankel  set theory, augmented with axioms for  classes  also, as  is presented for instance in bibliography [ Cohn P.M. 1965]  p.1-36  with  axioms A1-A11. Wee denote by  Ù1 the class of the ordinal numbers. (The last   capital   letter   of   the   Greek   alphabet    with subscript 1). The axioms A1-A11 allow for larger entities than sets, to define  algebraic fields or integral  domains  or  semi-groups. Hence we will also study  classes  that  have  two  algebraic operations (Their Cartesian square treated as classes of sets of the form {{x, y}, {x}}, that is  of  ordered  pairs)  that satisfy the axioms of an algebraic field and have a  subclass called the class of positive elements, with properties 1. 2., that they define a compatible ordering in the field (again as a class of ordered  pairs)  such  classes  that  are  ordered fields we will call again ordered fields and if we  want  to discriminate them from set-fields, especially when  they  are classes that are not sets, we will write for them  that  they are  c-fields  similarly  we  write  c-integral   domains  or c-semigroups. We must not confuse the term "c-field" with the term "class-field" of  the  ordinary  set-fields  of  "class-fields  theory"  (see  [ Van der Waerden B.L 1970],  [Artin E.-Tate J. 1967]). A   subset (or  subclass) denoted by X Í F of a linearly ordered field F, is said to be cofinal with F, if for every a Î F there is a bX with a£b.

    Definition 1. We say that an ordinal number á' is contained in a linearly  ordered  field  (or  integral  domain  or  double abelian monoid ) denoted by F, if there is an ordinal á, á'<á and , where x is an ordinal ,and a subset A of F+È{O} and  a  function h: W(á) = W{ á }® A which is an order isomorphism  (similarity) of W(á) and A and such that h(0)=0 and  if  â  is  an ordinal number with â<á  then h(s(â))=h(â)+1 in  the  field operations and furthermore the set A is  closed  to  sum  and product in the field (integral   domain   or   double   monoid)   operations   and isomorphic by h  to  the  W(á)  relative  to  the  Hessenberg natural operations .

Remark 2. If an ordinal number á’ is contained in the field F, then also the sequent of á’, S(á’)  is  contained  in  F.  This holds since the sequent of á' is again in W(á) where á as in the definition above.

Remark 3. If the ordinal number á is contained in  the  field F, then obviously every ordinal number less than á,  is  also contained in the field F. In the next, we will  suppose  (for simplification of symbolism) that if the  ordinal  á  is contained in F, the set á is á subset of F, and also  á  is  the element h(á) of the field F. We fix a mapping h for each ordinal that is contained in F .So we can talk about the set of ordinals contained in F as if it is a subset of F .The set of  ordinal  numbers  that  are contained in a linearly ordered  set-field,  is  obviously  a non-empty set. (Because as F is linearly ordered, charF = ¥ hence for every natural number n, we have that it is a (finite)  ordinal  contained  in  the field F).

But even more by the remarks 2, 3, we have that the set of  ordinals  contained in a linearly ordered field  ,which of course by the non-Neuman definition of ordinals is itself an ordinal , is  either of the form W(x) or W(x) È {x}  =  W(S(x)) for  some  ordinal number x  (in other words either it shall be a limit ordinal or it shall have a immediately  previous ordinal ).  The  last  case  is  directly excluded (by remark 2) hence it is of the form W(x) = x, that is this set is itself a limit ordinal  number.  In  case  the linearly ordered field F, is a c-field then all the  ordinals contained in F is again a set which is limit ordinal  number, or the class  Ù1 of all ordinal numbers.

Definition 4. Let a linearly ordered set-field  (or  integral domain or double abelian  monoid) demoted by  F.  Let  á  be the  set  of ordinals contained in F (which  is  itself  a limit  ordinal number). We say that the field (or integral domain  or  double abelian monoid ) F is of characteristic á and we shall write charF = á.

          If F is a c-field we include the case  of characteristic Ù1 and we write charF = Ù1 if all ordinals contained in F is the class Ù1 and also it is a cofinal subclass with F.

 

     Remark . In the case of a set-field F with  á  =  charF,  we do not need to suppose that the subset of elements of F corresponding to the ordinal in á by the definition 1 (it always exists ,by making use of the  definition by transfinite induction and its version that uses only  a  set of functions sufficient for an inductive  rule), see  appendix A), is cofinal with F, as this is a consequence of the definition. For, if there is an element  with â<X0 for  every  ordinal number â with â£a, then the set áÈ{X0} can be  extended , with the field operations ,to its closure  in the natural Hessenberg operations (a semiring) (see  [Kyritsis C. Alt] ) and  it becomes similar to an  initial segment of a principal  ordinal number   Thus á+1 is an ordinal contained in F, contradiction with  the definition of a .

By the previous definitions we realize that  every  linearly ordered set-field has characteristic which is  a  limit ordinal number.

          The  fact  that  the  linearly  ordered  field   F   has characteristic ù (the least infinite ordinal)  is  equivalent with the statement that the field F is Archimedean.

     In the followings when we will work  on  a  linearly  ordered field denoted by F of ordinal characteristic á, á=charF  (or Ù1= charF) we will supposed that is fixed  an  embedding  of the ordinal numbers of the initial segment w(á) in the set  F (or of  Ù1 in F).

     If the characteristic is ù, the embedding is obviously  unique as it can be proved by finite induction.

     Remark.5 Let a linearly ordered field denoted by F .Obviously there is an extension which is  a real field .Let us denote by R(F) the real closure of F .(For  results of the theory of Artin-Schreir  on real and real closed fields see e.g.[ Lang S. 1984] ch xi .or [Artin E.-Shreier O. 1927]) Since  R(F) can be obtained by adjunction of the square roots of the positive elements of F and Zorn's Lemma on  algebraic extensions see[Lang S. 1984] ch i proposition 2.10 theorem 2.11  pp 397), it is direct that the characteristic of the real closure R(F) is  the same with that of F.

     For  the  definitions  of the terms infinite,  finite, infinitesimal elements  in an extension of such fields, see e.g.[ Lang S] ch xi paragraph 1 pp 391, the definitions can be given relative to  extensions of any linearly ordered field to an other linearly ordered field ,and not only extensions  of the real numbers.

§2     The ordinal natural numbers N . The ordinal- integers Z .

          Let w(á) a principal initial segment of ordinal numbers. Let us denote by + and . the  Hessenberg's  natural  sum  and product in w(á). They satisfy properties 0.1.2.3.4.5.6. after lemma 1  in §1  in [ Kyritsis C.1991 Alter]

Definition 6. The set w(á)=á   where  for some  ordinal x, is an abelian double monoid  relative  to  sum and product and furthermore it satisfies the  cancellation  low  (see  [ Kyritsis C. 1991 Alter] lemma 1 ).This set I call the (double abelian) monoid of ordinal natural numbers  of characteristic a and I denote it by Ná. Thus Ná =á.

     Remark 7. It is obvious that the (double abelian, well ordered ) monoid Ná, is  the minimal  such  monoid  of  characteristic   á and the embedding of the ordinal numbers of W(á) in it is unique . Furthermore it can be proved by transfinite induction that it is a unique factorization monoid (called simply factorial monoid also).

     The   additive cancellation low in á   has as  a  consequence that á  is  monomorphicaly  embedded  in  its  Grothendieck group  denoted  by  k(á)  (see  [Lang S. 1984]  Ch.1  §9 p. 44). Furthermore the Grochendieck group k(Ná) can be ordered  by defining the set of positive elements k(á)+= {v/v  =  (x,y) with x,y w(á) and x > y }. We remind the reader  that if we  denote  by Fab(á) the free abelian group generated by á, and  by ((x+y)-x-y) the normal subgroup  of  Fab(á)  generated  by elements of the form (x+y)-x-y, then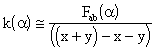              

          By (x,y) we denote the equivalence class that is defined in Fab(á) in the process  of  taking  the  quotient  group Fab(á)/((x+y)-x-y) by the representative x+(-y).

 The first part of property 6. (lemma 1  in  [Kyritsis C.1991 Alter]) guarantees that this ordering in k(á) restricted on  á  coincides with the usual ordering of ordinal numbers.

Definition 8. The ordered Grothendieck group  k(á)  of  an  initial segment of ordinals  relative to natural  sum, we call transfinite cyclic group of exponent á and we  denote it by Ãá. (by [Kuratowski K. Mostowski A. 1968] ch vii §7 pp 252-253 exercises 1.2.3.the ordinal á has to be of the type ùx. If the ordinal á is principal then I denote it also by Zá).

          Every element of  the  group  Zá is  represented  as  a difference x-y with x,yw(á). Then we define multiplication in Zá by  the  rule

 (*)  (x-y).(x'-y')=(x.x'+y.y')-(xy'+x'y)

where sum and product are the  natural  sum  and  product  in w(á). This makes Zá a commutative ring with unit (the element 1).

          If (x-y)(x'-y') = 0 and both (x-y), (x'-y') are not zero, we get by property 6 in lemma 1 in [Kyritsis C. 1991Alter] that xx'+yy' ¹ xy'+yx' or (x-y)(x'-y') ¹ 0, contradiction. Then one of

(x-y),(x'-y') is zero that  is the ring Zá has no divisors of zero and  it  is  an  integral domain. Remembering that Zá+ = {v|vZá and v = (x,+y) with x,yw(á)  x  >  y},  by property  6 lemma 1 in [ Kyritsis C. 1991 Alter],  we get  that  the  sum  and product of elements of Zá+ are again elements  of  Zá+.  From all these we get:

Lemma 9. The ring Zá is a linearly ordered  integral  domain of characteristic the principal ordinal á (see § 1 Def.1).The set Zá+ is a linearly ordered double abelian monoid and Zá+¹Ná

Definition 10 . The integral  domain  Zá I  call ordinal  integers of characteric á .

The integral domain Zá of characteristic  á  has  minimality relative to its property  of being an integral domain of characteristic á, in the following sense: Every integral domain of characteristic á contains a monomorphic image of Zá.

Theorem 11  (Minimality).

Every  integral domain Zá is  minimal  integral  domain  of  characteristic  á.  That is every  integral   domain   of characteristic  á, contains   a monomorphic image of Zá.

Proof. Put Rá an integral domain of characteristic á, where á is a principal ordinal number ().

Then the initial  segment  w(á)  is  contained  in  Rá (more precisely an order preserving image of w(á)).  The  principal initial segment is closed to the integral  domain  operations and by theorem 13,14 of [ Kyritsis C. 1991 Alter],  they coincide with the natural sum and product of Hessenberg. Then, applying the construction of this paragraph for the integral-domain Zá, we remain  inside  the integral-domain Rá, that is ZáÍRá. This proves the minimality.

Remark 12. The ordinal integers are  semigroup-rings of quotient monoids of semigroups that are used to define as semigroup-rings  the hierarchy of integral domains of the transfinite  integers  (see  [Gleyzal A. 1937]  pp  586).I  use  the term hierarchy not only as a well ordered sequence but also as a net (thus partially ordered ). The transfinite real numbers are thus  an  hierarchy.

The   transfinite   integers over   the  order-type ë symbolised by Z(ë), is the semigroup-ring (also module Z-algebra   and   integral   domain)   of    the     linearly ordered monoid  , where  is the coproduct, or direct sum denoted also  by ,  of a family of isomorphic copies of  N with  set of indices the order-type ë. Thus Z(ë) =Z[]. Thus any ring of  polynomials of a linearly ordered set of variables with integer coefficients is an integral domain of transfinite integers and conversely. It can be proved with  the  axiom  of  choice  and transfinite induction , as in  the  case  of finite  set  of  variables,  that Z(ë)  is  a  unique  factorization domain .  On  the other hand the Cantor normal form in the Hessenberg operations of the ordinal numbers (see lemma 6 in [Kyritsis C. 1991 Alter]) gives that any element x of Zá is of the form  xi are ordinals with x1>...>xn . The ordinal powers of ù in Zá is an abelian well ordered monoid (see e.g. [Neumann B.H. 1949] §2 pp 204-205) of ordinal characteristic â=ùx , if . Let us denote it by Mâ. Actually Mâ=â. Let us denote by , or simply by ëá the order type of the  Archimedean equivalent classes of Mâ. Then we get by the Cantor normal form that Zá =Z [Mâ] (The semigroup ring of Mâ). The monoid Mâ can be obtained as quotient monoid of the free abelian multiplicative  monoid of ëá variables, which is the monoid  .

 But Z []=Z(ëá), which  was  the assertion to  be  proved.

Remark 13 The equation  gives an alternative, simpler definition of the  ordinal integers without the use of the Hessenberg multiplication, since the ordinal powers of ù coincide n the abelian Hessenberg operations and the usual ordinal operations (see [Kyritsis C.1991 Alter] Remark 7.5) ) and without the use of the Grothentick group .The monoid Mx  is defined as the initial segment W(ùx) (or simply as the ordinal ùx) in the Hessenberg addition .

 

§3   The  definition  of  the  fields  Qá, Rá, Cá, Há.

In this  paragraph, I  shall  introduce  the  hierarchies  of fields of ordinal rational ,real, complex ,quaternion numbers. These hierarchies give the unification of the other three techniques and hierarchies, namely of the transfinite real numbers,  of  the  surreal  numbers. Furthermore   we  introduced the   hierarchies   of    transfinite complex and transfinite quaternion numbers.

Definition 14. The localization (field of  quotients)  of  the integral domain Zá, I  will denote by Qá  and  I  will  call ordinal  rational numbers (of characteristic á)  (see [Lang S. 1984] ChII §3).

Remark. Since we have that cancellation low holds,  we  do  not have to use the Malcev-Neuman theorem (see  [Cohn P.M. 1965]  Ch  VII  §3. Theorem 3.8). We define as set of positive element of Qá the set . It  is elementary in algebra that if the integral domain is linearly ordered then also its field of quotients (localization)  with the previous definition for its set of positive elements,  is a linearly ordered field with the restriction of its ordering on the integral domain to coincide with the ordering  of  the integral  domain.  Obviously  the  ordinals  of  the  initial segment of w(á) are contained in Zá and also in Qá. By a direct argument, holds also that the characteristic of Qá is a: Char Qá = á.

      Remark From the construction of Qá we infer easily that À(Qá) = À (á) and if á < â where á, â are two principal ordinals then QáÍQâ. The converse obviously holds.

Lemma 15. Every element  x  of  the field  Qá is of the form   where ái, âj  w(á) and  á1>á2>...>án³0,  â1>â2>...>âm³0  and ai, bj  for i = 1,...,n, j = 1,...,m are finite integers.

Proof.  Direct  from  the  definition  of  localization   and lemma 6 in [ Kyritsis C. 1991Alter].

Theorem 17. (Minimality)

The field Qá is a minimal field of characteristic á, in the sense that every field of  characteristic  á,  contains  the field  Qá (more precisely an order preserving monomorphic image of Qá).

Remark. This property is already obvious  for  the  field  of rational numbers, that in the  statement  of  Theorem  17  is denoted by Qù.

Proof. Let a field of characteristic á, that we denote by Fá. Then the  principal  initial  segment  w(á)  of  ordinals  is contained in Fá and the field-inherited operations  coincide with the natural sum and product of Hessenberg  (see  theorem 14 in [ Kyritsis C. 1991 Alter]). Then constructing  first  the  integral  domain Zá  and afterwards its localization Qá we always remain in the  field Fá.

          Thus Qá Í Fá (or more precisely h(Qá) Í Fá where h is  a order-preserving monomorphism of Qá in to Fá)                  q.e.d.

Definition  18.  The  (strong)  Cauchy  completion   of   the topological field Qá we denote by Rá and I  call  ordinal real numbers of characteristic á.

Remark.The process of extensions ,beginning with a principal initial ordinal á=Ná which is  the  minimal  double, abelian monoid of characteristic  á,  and  ending  with  the  field  Rá which is the maximal field of characteristic á ,we call K-fundamental densification .

Lemma 19. The  characteristic of the (strong) Cauchy completion of a linearly ordered field F ,is the same with that of the field F.

Proof. If the characteristic ofthe field is á, let us denote it by Fá, and its completion by . Obviously the characteristic of is not less than á.

Suppose that  there  is  an  ordinal  â  with á < â which  is contained in (see Definition 1). Then there  is  a  Cauchy net {xi|i  I} of elements of Fá that converges  to . Let å  Fá 0<å<1, then there is i0  I such that for every i  I i ³ i0

xi  (b-å, b+å) . But this gives an element of Fá greater than á, hence than every element of Fá, which is a contradiction. Thus Char Rá = á.                               q.e.d.

Corollary 20. The characteristic of Rá is á .

From the definition of Rá we infer that  À(Rá) £ 2À(á) and that á<â Û Rá  Râ for two principal ordinals denoted  by á, â.

Remark.21 We denote by R(ë) the transfinite real numbers of order-base ë . It holds by  definition that R(ë)=R((LRë)), where LRë is the lexicographic product of a family of isomorphic copies of the real numbers R ,with set of indices the order-type ë.

Remark . It is said that a field  F has formal power series representation, if there is a formal power series ring R((G)) and a ideal I of it such that F has a monomorphic  image in R((G))/I .From the universal embedding property of the hierarchy of transfinite real numbers we get that every linearly ordered  field has formal power series representation .Thus:

Corollary 22. The fields of ordinal real numbers R, have formal power series representation ,with real coefficients.

Definition 23 The field  Cá =  Rá[i] I call  ordinal  complex numbers  of characteristic á.

Definition 24.  The    field   C(ë)= R(ë)[i] we call transfinite  complex numbers of base-order ë. Actually it is the field C(ë)=C((LRë)) .

Definition 25. The quaternion extension field  of  the  field Rá (or of Cá) by the units i, j, k with i2 = j2 = k2 = ijk =  -1, I call the ordinal quaternion numbers of characteristic á and  I  denote them  by  Há .  They  are  non-commutative  fields (following the terminology e.g. of A.Weil in [ Weil A. 1967]) that  are transcendental extension of the non-commutative  field  H  of quaternion numbers.

Definition 26 . The formal power series fields H(ë)=H((LRë)) we call transfinite quaternion numbers of base-order ë.

For a proof that H((LRë)) is a (non commutative ) field see [Neumann B.H.1949] part I.

§4 The ordinal p-adic numbers Qá,p .

      As it is known  if F is a linearly ordered field ,and K a linearly ordered subfield of the real numbers and F½K  is an extension respecting  the ordering, then this extension defines the order-valuation (see [N.L.Alling 1987] ch 6 § 6.00 pp 207) .Actually every extension of any two linearly ordered fields  F, K, KÍF, respecting the ordering, defines a place, thus a valuation v. (I use the place and valuation as  are defined e.g. by O.Zariski in [Zariski O.-. Samuel P.1958] vol ii ch vi §2, §8.and not as are defined by A.Weil  in  [Weil A. 1967] ch iii  or  by v.der Waerden in [Van der Waerden B.L. 1970] vol ii ch 18 .The definition of Zariski is equivalent with the definition of v.der Waerden only for the non Archimedean valuations of the latter).

The place-ring is the Fí ={x/x  F and there are a, bK with a<x<b }. The maximal ideal of the place (or valuation v ) is the ideal of infinitesimals of K relative to F.

This valuation  we  call  extension - valuation  (and the corresponding place extension - place) It  has as special case the order valuation .The rank of the extension- place (see [Zariski O.-. Samuel P.1958] vol.II §3 pp 9) we call the rank of the extension .If char(F)>char(K) then the extension is transcendental ,and has transcendental degree and basis ;the latter is to be found in the ideal of infinitesimals or in the set of infinite elements .

Definition 27 .

          Let F a field of ordinal characteristic. Let R a subring of F that has F as its field of  quotients.  Let  p  a  prime ideal of R, such that the triple (pRp, Rp, F) where Rp  is the localization of R at p, defines a place of F.  Such  a  place (or valuation denoted by vp) I call p-adic of the field F. In  the  valuation topology of the valuation vp, that has a local base of zero  the ideals of R ) the field F is a topological field and the (strong) Cauchy completion I denote by Fp, it is a (topological field )  and I  call  p-adic extension field of F.

Definition 28. For F=Qa and R=Za in the previous definition the   field   Qá,p I   call   ordinal p-adic numbers    of characteristic á.

Final  remark  .Using  inductive  limit  ,or  union  of   the elements of the hierarchies of the previous ordinal and transfinite number systems, we get corresponding classes of numbers .The classes of ordinal natural, integer, rational, real, complex, quaternion numbers denoted respectively by Ù1, (or On ), Ù1Z, Ù1Q, Ù1R, Ù1C, Ù1H.

And the classes of transfinite integer, rational, real, complex, quaternion numbers denoted respectively by:

     CZ, CQ, CR, CC, CH.

Acknowledgments. I would like to thank professors W.A.J.Laxemburg and A.Kechris (Mathematics Department of the CALTECH) for the interest they showed and that they gave to me the opportunity to lecture about the ordinal real numbers in CALTECH. Also the professors H.Enderton and G.Moschovakis (Mathematics Department of the UCLA) for their interest and encouragement to continue this project.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

             

 

 

 

 Bibliography

[ N. L. Alling  1987]                                   Foundations of analysis over surreal number fields North-Holland  Ìath.Studies V. 141 1987 .

[ Artin  E.  Schreier   O.1927]                     Algebraishe konstruktion reellerkorper, Abh. Math. Sem.Univ. Hamburg 5 (1927) pp 85-99  .

[Artin E. - Tate J.1967]                              Class  Field   Theory  Benjamin 1967.

[Bourbaki N.1952]                                     Elemente de Mathematique algebre, chapitre II Hermann Paris 1948, chapitre VI Hermann                                    Paris 1952.

[ Clliford   A. H.1954]                                Note  on  Hahn's  theorem  on ordered  abelian groups. Proc. of the Amer. Math. Soc. 5 (1954) pp 860-863.

[ Cohen L.W. - Goffman C. 1949]              Theory of transfinite Convergence.Transact. of the Amer. Math. Soc. 66 (1949) pp 65-74.

[ Cohn P.M.1965]                                      Universal  Algebva Harper - Row 1965  .

[Conway J.H 1976].                                   On numbers and  games  Academic press 1976 .

[ Cuesta  Dutardi  N.1954]                         Algebra  Ordinal  Rev.  Acad. Cientis Madrid 4 (1954) pp 103-145 .

[ Dugundji J.1966]                                      Topology, Allyn and  Bacon  inc. 1966.

[Ehreshmann Ch 1956].                              Categories et structure Dunod  1956

[Ehrlich P.1988]                                         An alternative construction of Conway's Ordered Field No, Algebra Universalis                                    25  (1988) pp 7-16 .

[Ehrlich P ].                                                The Dedekind completion of No, submitted to Algebra Universalis.

[Endler  O.1972]                                        Valuation  Theory,   Springer 1972.

[  Erdos P.-Gillman L.-                               An isomorphism theorem for real

        Henrkiksen  M.1955]                         closed fields.  Ann. of Math.(2) 61 (1955)pp 542-554.

[Frankel A.A.  1953]                                  Abstract  set  Theory.  North  - Holland 1953.

[Fuchs L 1963].                                          Partially ordered algebraic systems. Pergamon   Oxford 1963.

[Gillman L.-Jerison M.1960]                       Rings of continuous functions. Van Nostrand Princeton 1960.

[Gleyzal A.   1937]                                     Transfinite real numbers. Proc. of the Nat. Acad.of scien. 23 (1937) pp 581-587.

[Gravett K.A.H. 1956]                               Ordered abelian groups. Quart. J. Math. Oxford 7 (1956) pp 57-63.

[Hahn H.1907]                                           Uber die nichtarhimedishen Grossensysteme.S.  Ber. Akad. Wiss. Wein. Math. Natur.Wkl Abt.   IIa 116 (1907) pp 601-655.

[Hausner M.-Wendel J.G. 1952]                Ordered Vector Spases Proc. of the Amer. Math. Soc.3 (1952) pp 977-982.

[Hessenberg G.  1906]                               Grundbegriffe  der  Mengenlehre (Abh. der  Friesschen Schule, N.S. [1] Heft 4) Gottingen 220 1906).

[Hilbert D.1977]                                         Grundlagen der Geometry Teubner Studienbucher 1977 .

 [Hilbert D. -Ackermann W.1950]              Principles of Mathematical Logic. Chelsea  Pub. Comp. N.Y. 1950.

[Kaplansky I. 1942]                                   Maximal fields with valuations Duke  Math.  J.  9  (1942)   pp 303-321.

[Krull W.  1931]                                         Allgemeine Bewertungs theorie. J.reine angew. Math. 176 (1931) pp 160-196.

[Kuratowski K 1966].                                Topology  v.I   v.II   Academic Press 1966.

[Kuratowski K. -Mostowski A.1968]         Set  Theory  North  -  Holland 1968.

 [Kyritsis C.E.1991]                                   Alternative algebraic definitions of the Hessenberg operations in the ordinal numbers. (unpublished yet).

[Lang S 1984].                                           lgebra .  Addison-Wesley   P.C. 1984 .

[Laugwitz Detler 1983]                               Ù Calculus as a  Generalization of  Field Extension.  An alternative   approach   to non-Standard  analysis  "Recent developments  in   non-standard analysis" Lecture Notes in Math 983   Springer 1983.

[MacLane  S.  1939]                                  The  Universality  of  Formal Power Series fields.Bull. of the Amer. Math. Soc. 45  (1939) pp 880-890.

[MacLane S 1971].                                    Categories for the working mathematician  Springer 1971

[Monna A.F.1970]                                     Analyse non-Archimedienne Springer 1970.

[Munkress J.R. 1975]                                 Topology. Prenctice Hall 1975.

[Nachbin  L. 1976]                                     Topology   and   Order.   Robert E.Krieger P.C. N.Y. 1976.

[Neumann B.H 1949].                                On ordered division rings. Transact. of the Amer. Math. Soc. 66 (1949) pp 202-252.   .

[Robinson A. 1974]                                    Non-Standard analysis.  North  - Holland 1974 (1966).

[Rudin W. 1960]                                        Fourier  analysis on groups. Interscience Pub 1960 .

[Shilling O.F.G.   1950]                              The theory of valuastions. Amer. Math. Soc. 1950.

[Schubert  H.1972]                                     Categories Springer 1972.

[Sirkoski R. 1948]                                      On an ordered algebraic field. Warsow, Towarzytwo Nankowe Warzawskie 41  (1948) pp 69-96.

[Stone A.L.  1969]                                     Non-Standard analysis in  topological algebra in Applications of Model Theory to Algebra,                                    Analysis and  Probability  N.Y. (1969) PP 285-300.

[Stroyan, K.D. and                                     Introduction to the  theory  of Infinitecimals

       Luxenburg W.A.J. 1976]                     N.Y.1976.

[Lynn A.Steen-                                           Counterexamples in Toplogy Springer 1970.

        Seebach J.A. Jr. 1970]            

[Van der Waerden B.L.1970]                     Algebra V1  V2 Frederick  Unger Pub. Co. N.Y. 1970.

[Weil A.1967]                                            Basic Number  Theory, Springer Verlag Berlin, Heidelberg  N.Y. 1967.

[Zakon E.1955]                                          Fractions  of  ordinal numbers Israel Institute of Tecnology Scient. Public. 6, 94-103 1955.

[Zariski O. -Samuel P.1958]                       Commutative Algebra V.I.II Springer 1958.

 

     List of special symbols

     ù           :  Small Greek letter omega,  the  first  infinit number.

 

     á, â        :  Small Greek letter alfa, an ordinal.

 

      Ù0         :  Capital   Greek   letter   omega   with    the superscript zero.

 

     Fa          :  Capital letter with superscript  a.  The of algebraic elements of a field F.

 

     char F      :  The characteristic of a field denoted by F.

 

     @           :  Equiralence relation of Kommensuvateness.

 

     ~           :  Equiralence relation of comparability.

 

     tr.d.(x) :  The transcendance degree initial of  words tr.(anscendance) and d.(egree).

 

     N(x)     :  Aleph of x, the cardinality of the set X. N: the fisrt capital letter of the Hebrew alfabet.

cf(X)=cf(Y) :  The sets x and Y are cofinal.

 

    W(á)        :  Initial segment of  ordinal  naumbers  defined by the ordinal number a.

 

            :  Natural sum and product of G. Hessenberg plus and point in parenthesis.

 

     Ná,Zá,Qá,Rá,:  Double-lined  capital  letters  with subscript small Greek letters

     Cá,Há           namely transfinite positive integers, intergals, rationals reats, complex and quatenion numbers.

 

     Zá1*ù      :  The dual lually compact abelian groups of  the transfinite integers Za. The capital letter  Z double-lined wiuth subscripts two  Greek  let-á (alpha) and ù (omega) and superscript a star

 

     Tá          :  Transfinite circle groups:  Capital  letter  T with subscript a small Greek letter.

 

     *X, *R et.c  :  A non-standard enlergement  structure  capital letter X with left superscript a star.

 

     îNo         :  A sureal number field of  characteristic  î. A small Greek letter followed by the symbol No.

 

     C,RC*R,No   :  The c-structures  (classes)  previous  symbols following the capital

     CN,CZ,CQ,.     latin letter C

     CC,CH

                :  Strong Canchy  competition  of  a  topological space capital letter with cap.

 

     Ó             :  Capital Greek letter sigma symbol for summation.

 

            :  The open full-linary tree of leight a. Capital latin D with subscript a  small  Greek  letter and in upper place a small zero.

The  ordinal real numbers 1. The  ordinal characteristic .

 

                                          by

                                      Dr. Konstantin E. Kyritsis

                                        Mathematics Dept.

                                        University of the Aegean

                                        Karlovassi  GR 832 00

                                        Samos  Greece .

 

                              Abstarct

  In this paper are introduced the ordinal integers ,the ordinal rational numbers ,the ordinal real numbers ,the ordinal p-adic numbers ,the ordinal complex numbers and  the  ordinal  quaternion numbers .It is also introduced the ordinal characteristic of linearly ordered fields. The final result of this series of papers shall be that the four different techniques  of  transfinite real numbers ,of non-standard enlargment fields of the real numbers ,of surreal numbers ,of ordinal real numbers give by inductive limit or union the same class of numbers known already as the class No and that would deserve the name the "finitary totally ordered Newton-Leibniz realm of numbers ".

 

 

 

 

 

 

 

 

 

                         Key words

Hessenberg natural operations in the ordinal numbers

principal ordinal

linearly ordered commutative fields

Grothendick group

archemidean complete fields

abstract additive valuation

formal power series fields

transfinite real numbers

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

APPENTIX  A.

A more effective form of Definition by transfinite induction.

1.Given a set z and an ordinal a ,let F be a  set  of  j-sequences with the properties:

a) If feF  then f/     eF  for every j in the domain of f.

b)For every j<a there is at least one feF  with j=w(j)=domain(f)   and values belonging to z.

c)If f  is an a-sequence of j-sequences of F  such that whenever g<j ,j <a  ,f       =f       ;then the a-sequence c (j)=f (j), belongs to F  also.

For each function hez  ,there is  one  and  only  one  transfinite sequence f defined on j<a , feF  and such that  f(j)=h[f/    ] for every j<a .

The function h is called a recursive rule for f. The set F with the properties a).b),c), is called ,sufficient  for recursive rules.

Proof: Not much different than the ordinary form od  definition  by transfinite induction .