Full Page
ORDINAL REAL NUMBERS 02
Free algebrae and alternative definitions of
the Hessenberg operations in the ordinal numbers .
By Dr.
Constantine E. Kyritsis
Department of Mathematics and Computer Science
Software Laboratory
Electrical and Computer Engineering
http://www.softlab.ntua.gr/~kyritsis
§0.
Introduction
This is the second paper of a
series of five papers that have as goal the
definition of topological complete linearly ordered fields (continuous
numbers) that include the real numbers
and are obtained from the ordinal numbers in a method analogous to the way
that Cauchy derived the real numbers
from the natural numbers. We may call them linearly ordered Newton-Leibniz
numbers. The author started and completed this
research in the
It is a wonderful perspective to try to define the Dirac’s deltas as natural entities of such stochastic real numbers. If in the completion of rational numbers to real numbers we ramify the equivalence relation of convergent sequences to others that include not only where the sequences converge (if they converge at the same point) but also how fast (if they converge in the same way ,an attribute related also to computer algorithms complexity) ,then we get non-linearly ordered topological fields that contain ordinal numbers (certainly up to ùa , a= ùù) and are closer to practical applications. This approach does not involve the random variables at all, but involves directly sequences of rational numbers as "Newtonian fluxions". This creation can be considered as a model of such linearly ordered fields (up-to-characteristic ùa , a= ùù) ,when these linearly ordered fields are defined axiomatically. This gives also a construction of the real numbers with a set which is countable. This does not contradict that all models of the real numbers are isomorphic as the field- isomorphism is not in this case also an Î-isomorphism so the Cauchy-real numbers and such a model still have different cardinality.
If we want to define in this way all
the Ordinal real numbers, then it is still possible but then this would give
also a device for a model of all the ZFC-set theory! And such a model is indeed
possible: By taking again sequences of non-decreasing (in the inclusion) finite
sets of ZFC , and requiring that any property ,relation or operation if
it is to hold for this set-sequence it must hold finally for each term of the
sequence and finite set. In other words we take a minimality for every set of
it, relative to the axiom of infinite. It is easy to prove that the (absolute)
cardinality of such a model is at most 2ù , that is at most
the cardinality of the continuum. We could conceive such a model as
the way a computer with its algorithms , data bases tables etc would
represents sets of ZFC in a logically consistent way. There is no contradiction with the 2nd-incompletness
theorem of Gödel as the argument to prove that it is a model of ZFC-set
theory is already outside ZFC-set theory (as are also the arguments of
Gödel ,or of Lowenheim-Skolem that
gives a countable model of ZFC-set theory).
In
this second paper on the same subject, I shall give two more ,and even simpler,
algebraic characterizations of the Hessenberg
natural operations in
the ordinal numbers. These characterizations are
actually alternative and direct definitions of the Hessenberg natural
operations; independent from the standard non-commutative operations
in the ordinal
numbers .The main results are
the characterization theorems
4.7.
.These
characterisations of the Hessenberg natural operations are :
a)
As operations defined by
transfinite induction through
two inductive rules that
are already satisfied
by the usual
operations in the natural numbers .
b)
An initial segment of a
principal ordinal 
in the
Hessenberg natural operations is isomorphic with
the free semiring
of á many generators in the
category of abelian semirings
;or isomorphic with the algebra
of polynomial symbols of á inderminates of the type of algebra of semirings
with constants the natural numbers .
The
previous characterizations proves that the Hessenberg natural operations are
the natural extensions in the ordinal numbers, of the usual operations in the
natural numbers,. This turns out to be so, if
we approach this subject from whatever aspect. Thus the Hessenberg
natural operations should be coined as the standard abelian operations in
the ordinal numbers,
for all practical algebraic purposes .There are
already extended applications of this . (see
[ Conway J.H.])
The
main application of the previous results is in the theory of ordinal real
numbers (see [ Kyritsis C.E. ] ).The final
result is that the three Hierarchies and different techniques of
transfinite real numbers (see [ Gleyzal A. ]), of the surreal numbers (see [ Conway J.H.]) ) ,of the ordinal real numbers (see [ Kyritsis C.E. ]) give by inductive limit
or union the same class of
numbers ,already known as the class
No and to which we make reference in [ Kyritsis C.E. ] as the "totally ordered Newton-Leibniz realm of numbers
".
§1.The
third algebraic
characterizations of the
Hessenberg natural operations.
Let
a initial segment of an ordinal number
of type â=ùá. Let us define a binary
operation ,denoted by +, in W(â) by definition by transfinite induction
(see e.g. [Kuratowski K.-Mostoeski A.] §4 pp 233, [Enderton
B.H.], [ Frankel A.A.], [Kyritsis C.E.] Lemma 2, 3 ) and the inductive rule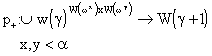 
defined by p+
(f)=S({f(W(x),y)}È{f(x,W(y))}) for an 
.
The definition
by transfinite induction
is supposed of two
variables as is also the inductive rule
(see [ Kyritsis C.E] Lemma 2,3). Thus, there exists a unique function
denoted by (+):W(ùá)2 ®W(ã+1),
where the ã is an
ordinal number with
ùá
<ã such that
it satisfies the inductive rule p+
; thus it holds :
p+ x+y=S({x+W(y)}È{{W(x)+y})
.
The restriction
of this operation in W(ù)=ù coincides with the usual
operations of the natural
numbers, since the addition of
the natural numbers satisfies also the inductive rule p+
:
Lemma 0. The Hessenberg natural sum in a initial
segment W(ùá ), satisfies
the inductive rule p+ .
Proof: See [
Kyritsis C.E] Proposition 8; the
arguments hold also for the initial segments of type W(ùá); if we
are concerned only for the natural sum . Q.E.D.
Thus
by the
uniqueness ,the natural
sum coincides with
the operation defined with the inductive rule p+.
Corollary 1.The operation defined as before by
the inductive rule p+, satisfies the properties 0.1.2.3.5.6.7.(See [ Kyritsis C.E]
lemma 1, the part of the properties that
refer only to the sum ).
Proof: See again
the [ Kyritsis C.E] proposition 8.
Q.E.D.
Since the
commutative monoid W(ùá) relative
the Hessenberg natural sum
satisfies the cancellation law, it has a
monomorphic embedding in the Universal group of it, which at this case is called also the
Grothendick group and it is denoted by K(W(ùá)). Thus the difference
x-y is definable in W(ùá) with values in K(W(ùá)).
See
also [ Kyritsis C.E] the remark before the proof of the proposition 8. Let an
initial segment W(ùá) of a
principal ordinal number . Let the binary operation denoted by (.):W()2®W(ã) ,where the ã is an ordinal number with <ã defined with
definition by transfinite
induction and with inductive rule the
function
p
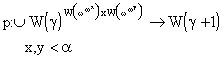such that for every
p
(f)=S({f(x,W(y))+f(W(x),y)-f(W(x),W(y)}Ç W(ã+1)) .
Thus there is a unique function (.):W()2 ®W(ã+1) such that it satisfies the inductive rule
p x.y=S({W(x).y+x.W(y)-W(x).W(y)}ÇW(ã+1)).
Lemma 2.The Hessenberg natural product
satisfies the inductive rule p .
Proof: See [
Kyritsis C.E]Proposition 8 . Q.E.D.
Therefore by the uniqueness of the function (.) this
operation coincides with the Hessenberg natural product .
Corollary
3.
Let an initial segment of a principal
ordinal number . The operations
that are defined
as before with the inductive
rules p+, p satisfy the properties 0.1.2.3.4.5.6.7.8. (See [ Kyritsis C.E] lemma 1)and coincide with the Hessenberg natural sum and
product .
Proof: See again [
Kyritsis C.E] proposition 8.
Corollary 4. (third characterisation)
Let
an initial segment of a
principal ordinal number
. Two operations in W() are the Hessenberg natural operations if and
only if they satisfy the inductive rules p+, p.
Proof:
Direct from lemma 2 and corollary 3. Q.E.D.
§
2 .The definition of the Hessenberg
natural operations with finitary free algebras .
In this paragraph we
shall prove a
key result with respect to the Hessenberg natural
operations. We shall prove that the Hessenberg operations are
actually free finitary operations definable by the operations of the Natural
numbers .
(see
[ Graetzer G.] about operations of polynomial symbols ch 1 e.t.c.)
Proposition 5.
Let an initial segment W(ùá) of an ordinal number of type ùá.
The commutative monoid W(ùá)
relative to the
Hessenberg natural sum is isomorphic with the commutative free monoid 
in the category of commutative monoids .
Remark: The free monoid coincides with the polynomial algebra of polynomial symbols
of the algebra of type (N0,.),in other words of commutative monoids
with nullary operations the constants of N0. Since the commutative
monoids is an equational class (variety ) there are free commutative monoids ;(see
[ Graetzer G.] ch 4 §25 corollary 2 pp 167
).
Proof: Let us define a function h : ®W(ùá)
by h(x)=ùx for x<á and h(n1x1
+...+nkxk)=n1ù1x +...+ nkùkx for any y=n1x1 +...+ nkxk
. The operations in the second part of the defining equation
of h are the Hessenberg natural operations .By the definition of and the Cantor normal form of ordinal numbers in the
Hessenberg operations we get that the h is 1-1 on-to and homomorphism of
abelian monoids .Thus an isomorphism of commutative monoids . Q.E.D.
Remark
6.
We deduce from the previous proposition that two initial segments W(ùá),
W(ùâ) are algebraically isomorphic as commutative monoids if and
only if À(á)=
À
(â), in other words the ordinals á, â have the same cardinality .
Proposition 7. (Fourth characterisation
) Let an
initial segment W() of a principal ordinal number . The commutative
semiring W() relative to the Hessenberg natural operations is
isomorphic with the commutative free semiring
N0 
in the category of commutative semirings with unit .
Remark : The free
commutative semiring with unit N0 coincides with the polynomial algebra of polynomial symbols
of the algebrae of type (N0,+,.) in other words of the commutative
semirings with nullary operations the constants of N0. The
commutative semirings with unit are an equational class thus they have free
semirings;
(see
again [ Graetzer G.] ch 4 §
25 corollary 2 pp 167 ).The semiring N0 is constructed as
the semigroup semiring
of the semigroup written
multiplicativelly;(in a way analogous to the construction of the
semigroup ring of a semigroup ).
Proof:
Let us define a function as in the proof of proposition 5
h2
:N0 ®W() by h2 (x)=ùh(x) for 
where the h is as in
the proof of the proposition 5 h : ®W(ùá)
and the is written multiplicatively; y
y= n1x1 +...+nkxk with x1,...,xk h(y)=
. Again by the definition of the N0 and the uniqueness of the Cantor normal form in the
Hessenberg natural operations (see [Kyritsis C.E.] Remark 7,5),b)) we get that
the function h is an homomorphism of semirings,1-1 and on-to ;thus an
isomorphism of abelian semigroups with unit . Q.E.D.
Remark 8.From the previous proposition and the
dependence of the free semiring N0 , up-to-isomorphism,on the cardinality of the set á, we
deduce that two initial segments W() , W(
) are algebraically isomorphic relative to the Hessenberg
natural operations if and only if À(á)=À
(â); n other words if the ordinal numbers á, â are of the same cardinality .
Bibliography
[ Bourbaki N. 1952] Elemente de Mathematique algebre, chapitre III Hermann Paris 1948, chapitre VI
Hermann Paris 1952.
[ Cohn P.M. 1965] Universal Algebva
Harper - Row 1965 .
[
[ Enderton B..H.1977 ] Elements of set theory Academic Press 1977 .
[ Frankel A.A.
1953] Abstract set
Theory. North -
[ Gleyzal A.1937 ] Transfinite real numbers. Proc. of the Nat. Acad.of scien.
23 (1937) pp 581-587.
[ Gratzer G. 1979] Universal Algebra . Springer-Verlag 1979
[ Hessenberg G.
1906] Grundbegriffe der Mengenlehre (Abh.
der
[ Hilbert D. -Ackermann W. 1950] Principles of
Mathematical Logic. Chelsea Pub.
[ Kuratowski K. -Mostowski A.1968 ] Set
Theory North -
[ Kyritsis C.E.,1991 ] Algebraic characterizations of the
Hessenberg operations in the
ordinal numbers .
[ Lang S.1984
] Algebra . Addison-Wesley P.C. 1984 .
[ Laugwitz Detler,1984 ] V
Calculus as a Generalization of Field Extension. An alternative approach
to non-Standard analysis "Recent developments in
non-standard analysis" Lecture Notes in Math 983 Springer 1983.
[ MacLane S.1939 ] The Universality of
Formal Power Series fields.Bull. of the Amer. Math. Soc. 45 (1939) pp 880-890.
[ Manin Yu.I. (transl. Koblitz.)N.1977 ] A course in Mathematical Logic Springer 1977.
[ Monna A.F. 1970] Analyse non-Archimedienne Springer 1970.
[ Neumann B.H. 1949]
On ordered division rings. Transact. of
the Amer. Math. Soc. 66 (1949) pp 202-252.
[ Robinson A,1966]. Non-Standard analysis.
North -
[ Zakon E.1955
] Fractions
of ordinal numbers Israel
Institute of Technology Scient. Public.
6, 94- 103 1955.
Free algebras and alternative
definitions of the
Hessenberg operations in the
ordinal numbers .
by Dr. Konstantin E. Kyritsis
Mathematics
Department, University of the
Karlovassi GR_832 00
Abstract.
It is proved and is given, in this paper, two alternative algebraic definitions of the Hessenberg
natural numbers in the
ordinal numbers:
a)
by definition with
transfinite induction and two inductive rules ,
b) by
the free algebras
of the polynomial
symbols of the commutative semirings with unit .
Key Words
Hessenberg
natural operations
ordinal numbers
free algebras
semirings