Full Page

ORDINAL REAL NUMBERS .00

Alternative algebraic definitions of the Hessenberg

natural operations in the ordinal numbers .

By Dr. Constantine E. Kyritsis

Department of Mathematics and Computer Science

University of Portsmouth

Software Laboratory

Electrical and Computer Engineering

National Technical University of Athens

http://www.softlab.ntua.gr/~kyritsis

kyritsis@softlab.ntua.gr

§0. Introduction This is a series of five papers that have as goal the definition of topological complete linearly ordered fields (continuous numbers) that include the real numbers and are obtained from the ordinal numbers in a method analogous to the way that Cauchy derived the real numbers from the natural numbers.We may call them linearly ordered Newton-Leibniz numbers. The author started and completed this research in the island of Samos during 1990-1992 . Seven years later (1999) he discovered how such numbers can be interpreted as fields of random variables (stochastic real numbers) that links them to applications of Bayesian statistics, stochastic processes and computer procedures. From this point of view it turns out that the ontology of infinite is the phenomenology of changes of the finite. In particular the phenomenology of stochastic changes of the finite can be formulated as ontology of the infinite .He hopes that in future papers he shall be able to present this perspective in detail.

It is a wonderful perspective to try to define the Dirac’s deltas as natural entities of such stochastic real numbers. If in the completion of rational numbers to real numbers we ramify the equivalence relation of convergent sequences to others that include not only where the sequences converge (if they converge at the same point) but also how fast (if they converge in the same way ,an attribute related also to computer algorithms complexity) ,then we get non-linearly ordered topological fields that contain ordinal numbers (certainly up to ω^a , a= ω^ω) and are closer to practical applications. This approach does not involve the random variables at all, but involves directly  sequences of rational numbers as "Newtonian fluxions". This creation can be considered as a model of such linearly ordered fields (up-to-characteristic  ω^a , a= ω^ω) ,when these linearly ordered fields are defined axiomatically. This gives also a construction of the real numbers with a set which is countable. This does not contradict that all models of the real numbers are isomorphic as the field- isomorphism is not in this case also an Î-isomorphism so the Cauchy-real numbers and such a model still have different cardinality. If we want to define in this way all the Ordinal real numbers , then it is still possible but then this would give also a device for a model of all the ZFC-set theory! And such a model is indeed possible: By taking again sequences of non-decreasing (in the inclusion) finite sets of ZFC , and requiring that  any property ,relation or operation if it is to hold for this set-sequence it must hold finally for each term of the sequence and finite set. In other words we take a minimality relative to the axiom of infinite for every set of it. It is easy to prove that the (absolute) cardinality of such a model is at most 2^ω  , that is at most the cardinality of the continuum. We could conceive  such a model as the  way a computer with its algorithms , data bases tables etc would represents sets of ZFC in a logically consistent way. There is no contradiction with the 2nd-incompletness theorem of Gödel as the argument to prove that it is a model of ZFC-set theory is already outside ZFC-set theory (as are also the arguments of Gödel ,or of Lowenheim-Skolem that gives a countable model of ZFC-set theory).

In this paper are studied the Hessenberg operations in the ordinal numbers, from an algebraic point of view.

The main results are the characterisation theorems 9,10 . They are characterisations of the Hessenberg operations as

a) field-inherited operations in the ordinal numbers,that satisfy two inductive properties .(see proposition 10)

b) operations that satisfy a number of purely algebraic properties, that could be called in short operations of a well-orderd commutative semiring with unit ;(see Lemma 0, proposition 9).

In a next paper I shall give two more algebraic characterisations of the Hessenberg operations as

c) operations defined by transfinite induction in the ordinal numbers and by two recursive rules ,

d) operations of the free semirings in the category of abelian semirings; or as the operations of the formal polynomial algebras of the category of abelian semirings. These characterisations of the Hessenberg operations are independed of the standard non-commutative operations of the ordinal numbers and can be considered as alternative and simpler definitions of them (especially the c),d)).

In particular it is proved that the Hessenberg natural operations are free finitary operations ; We make use of rudimentary techniques relevant to K-theory and Universal Algebra .

The main application of the present results is in the definition of the ordinal real numbers.(see [ Kyritsis C.E.1991] .By making use of the present results and techniques it is proved in [Kyritsis C.E.1991] that all the three techniques and Hierarchies of transfinite real numbers ,see [ Glayzal A 1937],of surreal numbers, see [ Conway J.H. 1976], of ordinal real numbers see [ Kyritsis C.E.1991], give by inductive limit or union, the same class of numbers ,already known as the class No. We refer to the class No as "the totally ordered Newton-Leibniz realm of numbers").

1. Two algebraic characterisations of the Hessenberg operations in the ordinal numbers.

Let us denote by F a linearly ordered field of characteristic ω (also said of characteristic 0).Let us denote by h a mapping of an initial segment of ordinal numbers, denoted by W(a),in F such that it is 1-1, order preserving and h(0)=0, h(1)=1, h(s(b))=b+1,where s(b) is the sequent of the b , b<a, the b+1 is in the field operations the set h(W(a)) is closed in the field addition and multiplication . We shall call field-inherited operations in the ordinal numbers of W(a), the operations induced by the field, in the initial segment W(a).

(For a reference to standard symbolisms and definitions for ordinal numbers, see [Cohn P.M. 1965] p.1-36 also [ Kutatowski K.-Mostowski A. 1968]).

The following properties hold for these field-inherited abelian operations for the ordinals of w(a) ( in that case, it is needless to say that a is a limit ordinal).

Lemma 1. For the field-inherited abelian operations in the initial segment w(a) of ordinal numbers, the followings hold (x,y,z,c,x',y', Îw(a)).

0) s(x) = x+1 for every x Î w(a)

1) x+y = y+x , x.y = y.x

2) x+(y+z) = (x+y)+z , x.(y.z) = (x.y).z

3) x+0 = 0+x = x ,

x.0 = 0

x.1 = 1.x = x

4) x(y+z) = xy+xz

5)

6) If x>y, x'>y' then x+x'>y+y', and xx'+yy'>xy'+yx'

The proof of the previous lemma is direct from the properties of a linearly ordered field.

We mention two more properties that they will be of significance in the followings paragraphs.

7) The w(x+y) is a cofinal set with the {w(x)+x x+w(y)}and we write cf(w(x+y)) = cf{w(x)+y x+w(y)}.

8) The W(x.y) is cofinal set with the

h^-1({h(y)h(w(x))+h(x)h(w(y))-h(w(x)).h(w(y))})

and we write

cf(w(x.y)) = cf h^-1 ({h(y)h(w(x))+h(x)h(w(y))-h(w(x)).h(w(y))})

To continue our argument we need a many-variables form of transfinite induction.

Let a_i i = 1,...,n n N ordinal numbers and (b₁,...b_n) w(α_i)x...xw(α_n). We define as simultenous initial segment of n-variables defined by (b₁,...b_n), the set w((b₁,...b_n)) = w(b₁)x...x{b₁}x...xw(b_n) for every

I {1,...n},or w((b₁,...,b_n))= w{b₁}x...xw{b_i)x...x{b_n} for

every I {1,...n} with I ¹ Æ.

Lemma 2. (many-variables transfinite induction)

Let A w(a₁)x...xw(a_n) such that

1. (0,...,0) A

2. For every (b₁,...b_n) w(a₁)x...xw(a_n) it holds that w((b₁,...,b_n)) A Þ (b₁,...,b_n) A.

By 1.2. we infer that A = w(a₁)x...xw(a_n).

Lemma 3. (many-variables definition by transfinite

induction)

Let a set A and ordinal numberss a₁,...,a_n. Let a set denoted by B, such that it is sufficient for inductive rules h B®A :

This means that :

a)

The set B is a set of functions, denoted by and defined on simulteneous initial segments with values in A. : w((b₁,...,b_n)) ® A.

If B and c₁< b₁,...,c_n< b_n then B

b) For every there is a such that B

c) Let and let us denote the value of f at (b₁,...,b_n) with . Let us suppose that it holds that whenever c₁ £ b₁,b'₁,...,c_n £ b_n,b'_n, (b₁,...,b_n),(b'₁,...,b'_n)

w(α₁)x...xw(α_n) then

Then let us suppose that we get as a consequence that the function defined by , belongs to B

It holds that for every function h:B ® A

(called many -variables transfinite inductive rule ) there is one and only one function f defined on w(a₁)x...xw(a_n) with values in A such that for every (b₁,...,b_n) w(α₁)x...xw(α_n) it holds that

Remark:We notice that even for one variable this version of the definition by transfinite induction is somehow different from that which appears usually in the bibliography (e.g.see [Kutayowski K. –Mostowski A 1968] §4 pp 233 ).It uses not all the set A^w(α) ,but only a subset of it, sufficient for recursive rules .The proof ,for one variable, is nevertheless exactly the same as with the ordinary version .

In order to save space and because the proofs are not directly relevant to our subject we will not give the proofs of lemma 2 and 3 but we will mention that they are analogous, without serious difficulties, to the ones with one-variable only (see e.g. [ Kutayowski K. –Mostowski A 1968],[ Lang S.1984]).

Proposition 4. (Uniqueness)

Any two pairs of field-inherited operations in the initial segment w(a) of ordinals, satisfying properties 7,8 of lemma 1 (a is a limit ordinal ) are isomorphic .

Proof: Let a monomorphic embedding denoted by h of w(a), as is described in the beggining of the paragraph in two linearly ordred fields denoted by F₁, F₂.

Let the two pairs of field inherited operations in w(a) be denoted by ((+,.) () respectively. They satisfy the properties 0.1.2.3.4.5.6.7.8.of lemma 1 . Suppose that the operations +, coincide for the set where . Then by property 7 (by the hypothesis of transfinite induction) =

Where by S(A) we denote the sequent of the set A .Thus by lemma 2 the operations +, coincide on w(a)xw(a).

Then the set w(a) is an ordered abelian monoid relative to addition, with cancelation law.

The Grothendieck groups of w(a) for both +, and coincide, and we denote it by k(w(a)) (see for the definition of Grothendieck group [Lang S. 1984] Ch1 §4 p. 44 or [Cohn P.M. 1965] ch vii §3 pp 263 ). Thus also the opposite -x of an element x of w(a) is the same in the Grothendieck group k(w(a)) of w(a) for both the two operations + and .

Suppose also that the operations coincide for the set w ((b₁, b₂)). Then by property 8

(because +, and are isomorphic and the hypothesis of transfinite induction for . Hence by lemma 2 the two operations coincide on the whole set w(a)xw(a) Q.E.D.

The next step is to find the relation of field-inherited operations in an initial segment of ordinals with the Hessenberg operations . It will turn out that, if they satisfy the properties 7.8.of lemma 1 ,then they are nothing else than the Hessenberg-Conway natural sum and product (see [Kutatoski K.Mostowski A. 1968 ] ch VII §7 p. 252-253 exercises 1. 2. 3.) and [ Frankel A.A.1953] pp. 591-594 also [Conway J.H. 1976] ch2 p. 27-28).

The way in which the Hessenberg operations are defined, traditionally , depends on the standard non-commutative operation on ordinals.

In order to define the Hessenberg-Conway operations in the traditional way ,we remind that :

Lemma 6 (Cantor normal form).

For every ordinal a there exists a natural number n and finite sequences : b₁,...,b₂ of natural numbers and ordinal numbers a₁,a₂,...a_n with a₁>...>a_n such that (For a proof see for instance [Kutatowski K.-Mostowski A. 1968] ch VII §7 p. 248-251).

Then we get for the two ordinal numbers α, b, by adding terms with zero coefficients, to make their Cantor normal forms of equal length , that

we define the natural sum (we denote it by (+)) with The natural product, denoted by α(.)b is defined to be the ordinal arising by multiplication (using distributive and associative laws) from the Cantor normal forms of a and b and by using the rule: ω^x(.)ω^y =ω^x(+)y to multiply powers of ω. As a result we get for instance that

Remark 7

1) The normal form of a can also be written in the standard Hessenberg-Conway operations that is

2) The sum a(+)b is an increasing function of a and b.

3) If and then for ordinals ζ, η, α and conversely if an ordinal j satisfies the condition: "if ξ<j and η<j then ξ.η<j" then there exists an ordinal number α such that ;we call ordinal numbers of the type principal ordinals of the Hessenberg operations.(see [ Kutatowski K.-Mostowski A. 1968] ch vii paragraph 7,p 253) This has also as a consequence that we define the Hessenberg-Conway natural operations only for initial segments of the type Wfor some ordinal number α (we will call them principal initial segments ).

4) The Hessenberg-Conway natural operation restricted on the set of Natural numbers coincide with the ordinary sum and product of natural numbers.

5) The operation "powers of ω" , through the Hessendberg-Conway natural operation, can be defined as follows:

a) ω⁽⁰⁾ = 1 ω⁽¹⁾ = ω if ξ is a limit ordinal ω^(ξ) = sup ω^(η)

η<ξ

b) If ξ is not a limit ordinal then there exists an ordinal η with η(+)1= s(η)=ξ and we define ω^(ξ) = ω^η(.)ω.

It holds, (this happens especially for the base ω), that these "natural powers" of ω coincide with the standard powers of ω defined through the standard non-commutative multiplication of ordinal numbers (this can be proved with transtinite induction since ω^η.ω=ω^(η)ω. This gives us the right to express any ordinal number α in Cantor normal form, exclusively with natural operations:

6) Also we notice that, the natural difference denoted by a (-) b, of two ordinals a, b in Cantor normal forms

, is defined only if p₁³q₁... p_n³q_n.

7) We notice that if ξ_i<ξ_j for two ordinals then but also

for every pair of non-zero natural numbers a,b. (in the standard non-commutative operations on ordinals). But this has as consequence that the ordering of a finite set of ordinal numbers in Cantor normal form (normalizing the Cantor normal forms by adding terms with zero coefficients so that all of them have the same set of exponents) is isomorphic (similar) to the lexicographical ordering of the coefficients of the normal forms.

Proposition 8. For every principal initial segment of ordinal numbers, the Hessenberg natural operations satisfy the properties 0.1.2.3.4.5.6.7.8. of lemma 1.

Remark. From the moment we have proved the properties 0.1.2.3.4.5.6. for the natural operations in the principal initial segment w(a), there is the Grothendieck group k(w(a)) of the monoid relative to sum, w(a) such that the w(a) is monomorphicaly embedded in k(w(a) (because of cancelation law) and also there is an ordering in k(w(a)) that restricted on w(a) coincides with the standard ordering in w(a).

Then the difference that occurs in property 8 has meaning and also the statement of property 8 itself has meaning (see [Lang S. 1984] Ch I §9 p. 44).We denote by h the monomorphism of the W(a) in the K(W(a)) .

Proof. The properties 0.1.2.3.4. are directly proved from the definition of the natural operations. Let us check the property 5. Namely , the cancelation laws. Let us suppose that y,x,c, are ordinal numbers with y,x,c for some ordinal a and their Cantor normal form , in natural operations , are

p_i, c_i, y₁ No

then

hence

x(+)c=y(+)c Þ p_i +c_i = q_i +c_i i = 1,...,n

and by cancelation law for addition in natural numbers we deduce that p_i=q_i i=1,...,n hence x = y.

Also

and

and if c ¹ 0

and x(.)c = y(.)c then p_i.c_j = q_i.c_j with not all of c_j equal to zero. Say , then for every i = 1,...,n hence p_i = q_i and x=y.

Let us check the property 6. The first part of property 6 is immediate from Remark 7, 2. Let, furthermore, x',y' with Cantor normal form (changing the ξ_i, in order to have the same exponents for all x, y, x', y')

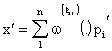
with p_i',q_i' No and with summation interpreted as natural sum. By hypothesis x'>y', x>y.

Then

and

and the coefficient of the monomial of greatest exporent of x(.)x'(+)y(.)y' is p₁p₁'+ q₁q₁' and of x(.)y'(+)y(.)x' is p₁q₁'+q₁p₁'. But p₁p₁' + q₁q₁' - p₁q₁' - q₁p₁' = p₁(p₁'-q₁') - q₁(p₁'-q₁') = (p₁-q₁). (p₁'-q₁') > 0 which is a product of the positive factors p₁-q₁, (p₁'-q₁') hence it is positive. By Remark 7,7 because p₁ q₁' + q₁ q₁' > p₁ q₁' + q₁ p₁ we deduce that x(.)x'(+)y(.)y'>x(.)y'(+)x'(.)y. Next we prove the property 7. Let x' as before but also satisfying x'w(x) that is x'<x. Then by property 5 we deduce that w(x)+yw(x+y). Conversely let z<x+y zw(x+y). Let the Cantor normal form of z be (we rearrange appropriately the normal forms of x, x', y, y', Z) with r_iNo. From the last inequality we get that in the lexiographical ordering it holds that (r_i,...,r_n)<(p₁+q₁,...,p_n+q_n)(*)

Let and

Let and Then the following ordinals are defined: z₁'(-)z, z₁'(-)y, z₂'(-)z, z₂'(-)y, and also by Remark 7,7. It holds that z£z₁' z£z₂', y£z₁' x£z₂'. From the inequality (*) and the inequality (**) q_i £ p_i + q_i i = 1,...,n and the definition of k_i we infer that it holds in the lexicographical ordering, the inequality (k₁,...,k_n) £ (p₁ +q₁,...,p_n + q_n) similarly (λ_i,…,λ_n) £ (p₁ + q₁,...,p_n + q_n). Hence by Remark 7.7. it holds that z₁'£x(+)y and z₂'£x(+)y If for both z₁', z₂' holds that z₁'=x(+)y=z₂'.

Then {r_i, q_i}={r_i, p_i}=p_i + q_i, hence r_i = p_i + q_i i=1,...,n.

But then z=x(+)y ,contradiction.

Let us suppose then, that z₁'<x(+)y.

Then if z" = z₁'(-)y by the last inequality we get that z"(+)y = z₁'(-)y(+)y = z₁' < x(+)y or z"(+)y < x(+)y.

That is we proved that for every zw(x+y) there is z" an other ordinal with z£z"(+)y<x+y. If z"³x then z"(+)y³x(+)y contradiction, hence z"<x that is z"w(x) and z"(+)yw(x)+y. From this and also that w(x)+yÍw(x+y) ,that we have already proved ,we deduce that w(x+y) and {w(x)+yÈx+w(y)} are cofinal sets; we write cf(w(x+y))=cf({w(x)+yÈx+w(y)}) . In other words we haved proved the property 7.

Let us prove the property 8. As we have already remarked the difference is to be understood in the extension of the additive monoid w(a) into the linearly ordered Grothendick group k(w(a)). The ordering in k(w(a)) is defined by: (x,y)£(x',y')Ûx+y'£x'+y.

Where by (x,y) we denote the equivalence class of the free abelian group generated by w(a), which is denoted by F_a,b (w(a)) (k(w(a)) = F_a,b (w(a))/ ([x+y]-[x]-[y])), in the process of taking the quotient by the normal subgroup generated by the elements of the form [x+y]-[x]-[y] in F_a,b (w(a)) (the corresponding generator of xw(a), in F_a,b (w(a) we denote by [x]), that is defined by the representative x+(-y). Needless to mention that the natural difference in w(a), isn't but an instance of difference in k(w(a)).

We make clear that h^-1({h(x)(.)h(w(y))(+)h(w(x))(.)h(y) -h(w(x))(.)h(w(y))}={v|vw(α) and v =h^-1 (h(x)(.)h(y)'(+)h(x')(.)h(y) - h(x')(.)h(y')) with x'w(x) y'w(y) and x,yw(a)}. By the property 6 we get that h(x)(.)h(y')(+)h(x')(.)h(y) < h(x)(.)h(y)(+)h(x')(.)h(y') hence

h(x)(.)h(y')(+)h(x')(.)h(y) - h(x')(.)h(y') < h(x)(.)h(y)

hence h^-1({h(x)(.)h(w(y))(+)h(w(x))(.)h(y) - h(w(x))(.)h(w(y))}} Í w(x(.)y).

Conversely, let, zw(x(.)y), that is z<x(.)y.

If x(.)y = then we also write for the normal form of

z: z = and r_ij No. By Remark 7,7. We deduce that in the lexicographical ordering it holds that (r₁₁,...,r_ij,...,r_n,n ) < (p₁p₁,...,p_ip_j,...,p_n.p_n). It is sufficient to prove that for every (r₁₁,...,r_ij,...,r_n,n) < (p₁p₁,...,p_ip_j,...,p_n.p_n) there are (p₁',...,p_n') and (q₁',...,q_n'), p_i, q_j No with (p₁',...,p_n') < (p₁,...,p_n) and (q₁',...,q_n') < (q₁,...,q_n) such that (r₁₁,...,r_ij,...,r_n,n) £ (p₁q₁'+p₁'q₁ - p₁'.q₁',...,p_n.q_n'+p_n'.q_n - p_n'.q_n') < p₁.q₁,..., p_n.q_n).

But the property 8 holds for a=ω, that is for the natural numbers. Hence there are p₁', q₁' with p₁' < p₁ q₁' < q₁ and r₁₁ £ p₁ q₁'+p₁'q₁ - p₁'.q₁' < p₁' q₁ and completing with arbitrary p_i', q_i' i = 2,...,n) that give positive the terms p_i q_j' + p_i'q_j - p_i'q_j' (by elementary arithmetic of natural numbers this is always possible) we define

x' = and y' = .

By the lexicographical ordering it holds that x' w(x), y' w(y) and h(z) £ h(x)(.)h(y')(+)h(x')(.)h(y) - h(x')(.)h(y') <h(x)(.)h(y). Hence the sets W(x(.)y) and h^-1({h(x)(.)h(w(y)) (+) h(w(x))(.)h(y) - h(w(x))(.)h(w(y))}) are cofinal and we write

cf(w(x(.)y)) = cfh^-1({h(x)(.)h(w(y)) (+) h(w(x))(.)h(y) - h(w(x))(.)h(w(y))}).

This is the end of the proof of the property 8. Q.E.D.

Corollary 9 (first characterisation )

Every pair of operations in a principal initial segment of ordinal that satisfy the properties 0.1.2.3.4.5.6.7.8 of lemma 1 ,.is unique up-to-isomorphism and coincides with the Hessenberg natural operations .

Remark: The difference that appears in the property 8 is defined as in the remark after the proposition 8 .

Proof:Direct after the proposition 4 and 8 Q.E.D.

.

Corollary 10.(Second characterisation )

Every pair of field -inherited operations in a principal initial segment of ordinals, w(a) that satisfy the properties 7. 8. coincides with the natural sum and product of Hessenberg .

( For the existence of field-inherited operations in the ordinal numbers see [C Conway J.H.1976 ] ch note pp 28 .)

Proof: The proof is immediate from proposition 4 and 8.Q.E.D.

Remark.11 It seems that N.L.Alling in his publications:

a)On the existence of real closed Fields that are η_α -sets of power ω_α Transactions Amer.Math.Soc. 103 (1962) pp 341-352.

b)Conway's field of surreal numbers. Trans.Amer.Math.Soc.287 (1985) pp.365-386.

c)Fountations of Analysis over Surreal number Fields .Math. studies 141 North-Holland 1987.

he is unaweare that if an initial segment of ordinals is contained in a set-field and it is cofinal with the field ,(and it induces the Hessenbeg operations in it) then it has to be an initial segment of a principal ordinal that is of type (see [Kutatowski K-Mostowski A.1968] ch VII §7 p. 252-253 exercises 1. 2. 3.)

Thus properties 0.1.2.3.4.5.6.7.8. can be taken as an axiomatic definition of the Hessenberg operations without having to mention the non-commutative ordinal operations.

In a forthcoming paper, I will be able to prove the non-contradictory of properties 0.1.2.3.4.5.6.7.8. (actually the existence in Zermelo-Frankel set theory, of the operations +,.) without using the non-commutative ordinal operations,neither field-inherited operations. but through transfinite induction and other methods of universal algebra .

Bibliography

[ Bourbaki N. 1952] Elemente de Mathematique algebre, chapitre III Hermann

Paris 1948, chapitre VI Hermann Paris 1952.

[Cohn P.M.1965] Universal Algebva Harper - Row 1965 .

[Conway J.H.1976] On numbers and games Academic press 1976 .

[Frankel A.A.1953] Abstract set Theory. North - Holland 1953.

[Gleyzal A. 1937] Transfinite real numbers. Proc. of the Nat. Acad.of scien. 23 (1937) pp 581-587.

[Hessenberg G. 1906] Grundbegriffe der Mengenlehre (Abh. der Friesschen Schule, N.S. [1] Heft 4) Gottingen 220 1906).

[Hilbert D. -Ackermann W.1950] Principles of Mathematical Logic. Chelsea Pub. Comp. N.Y. 1950.

[Kuratowski K. -MostowskiA.1968 ] Set Theory North - Holland 1968.

[Kyritsis C.E.1991 ] Ordinal real numbers I.II.III. (unpublished yet )

[Lang S.1984 ] Algebra . Addison-Wesley P.C. 1984 .

[ Laugwitz Detler 1983] Ω Calculus as a Generalization of Field Extension. An alternative approach to non-Standard analysis "Recent developments in non-standard analysis" Lecture Notes in Math 983 Springer 1983.

[ MacLane S.1939 ] The Universality of Formal Power Series fields.Bull. of the Amer. Math. Soc. 45 (1939) pp 880-890.

[ Monna A.F.1970 ] Analyse non-Archimedienne Springer 1970.

[Neumann B.H.1949 ] On ordered division rings. Transact. of the Amer. Math. Soc. 66 (1949) pp 202-252.

[ Robinson A.1974] Non-Standard analysis. North - Holland 1974 (1966).

[Zakon E. 1955] Fractions of ordinal numbers Israel Institute of Tecnology Scient. Public. 6, 94- 103 1955.

List of special symbols

ω : Small Greek letter omega, the first infinit number.

α, b : Small Greek letter alfa, an ordinal.

Ω₁ : Capital Greek letter omega with the subscript one.

À(x) : Aleph of x, the cardinality of the set X.

N: the fisrt capital letter of the Hebrew alfabet.

: Natural sum and product of G. Hessenberg plus and point in parenthesis.

Abstract

This paper proves prerequsite results for the theory of Ordinal Real Numbers. In this paper, is proved that any field-inherited abelian operations and the Hessenberg operations ,in the ordinal numbers coincide.It is given an algebraic characterisation of the Hessenberg operations ,that can be described as an abelian, well- ordered,double monoid with cancelation laws.

Key words

Hessenberg natural operations (in the ordinal numbers)

ordinal numbers

semirings

inductive rules

transfinite induction